The Elastic Coefficients of Double-Porosity Materials: A Revisit

Abstract

A strain-based constitutive model, i.e., the mixed stiffness formulation, is presented for a double-porosity material, and coefficients in these linear constitutive equations are identified. All six coefficients are determined by performing properly arranged thought experiments. Three long-time tests are first considered to obtain three independent equations. After that, an experiment to isolate the matrix material from the fracture behavior is performed to provide another four relations. Finally, a case in the long-time limit is considered to identify one of the off-diagonal coefficients in the formulation. In addition, as an example of application of the mixed stiffness formulation, the Navier- type equations are derived for wave propagation problems in double-porosity materials by reformulating the governing equations of some researchers.

Appendix: Pride’s Wave Equations for Double-Porosity Materials

As an example of application of the identified coefficients $b_{ij}$, we will use them to reformulate the governing equations, established by Pride and Berryman (2003a, b), for wave propagation in double-porosity dual-permeability materials.

The double-porosity theory for wave propagation has been reported by many researchers (e.g., Wilson and Aifantis 1984; Corapciouglu and Tuncay 1996, 1998; Berryman and Wang 2000; Pride and Berryman 2003a, b; Ba et al. 2011). Among them, the double-porosity, dual-permeability theory of Pride and Berryman (2003a, b) capable of modeling fluid transport between two porous phases has received substantial attention in recent years since it is increasingly believed that mesoscopic flow is a significant mechanism of fluid-related attenuation in the seismic band (e.g., Pride et al. 2004; Müller et al. 2010). Therefore, the governing equations of Pride and Berryman (2003a, b) will be chosen as an illustrative example to the application of the identified coefficients $b_{ij}$.

The macroscopic double-porosity governing equations established by Pride and Berryman (2003a) take the form (assuming a time dependence of the form $\exp (-i\omega t))$

$$\begin{aligned} \nabla \cdot {\varvec{\sigma }}= & {} -i\omega \left( {\rho \mathbf{v}+\rho _\mathrm{f} \mathbf{q}_1 +\rho _\mathrm{f} \mathbf{q}_2 } \right) , \end{aligned}$$

(82)

$$\begin{aligned} \left( {{\begin{array}{l} {\mathbf{q}_1 } \\ {\mathbf{q}_2 } \\ \end{array} }} \right)= & {} -\frac{1}{\eta }\left( {{\begin{array}{c@{\quad }c} {\kappa _{11} }&{} {\kappa _{12} } \\ {\kappa _{12} }&{} {\kappa _{22} } \\ \end{array} }} \right) \left( {{\begin{array}{l} {\nabla p_{\mathrm{f}1} -\rho _\mathrm{f} i\omega \mathbf{v}} \\ {\nabla p_{\mathrm{f}2} -\rho _\mathrm{f} i\omega \mathbf{v}} \\ \end{array} }} \right) . \end{aligned}$$

(83)

where $\mathbf{v}$ is defined as

$$\begin{aligned} \mathbf{v}\equiv \dot{\mathbf{u}}=-i\omega \mathbf{u}, \end{aligned}$$

(84)

$\mathbf{q}_1$ and $\mathbf{q}_2$ are, respectively, macroscopic fluid flux through the matrix and fracture phases, and $\kappa _{ij}$ are the permeabilities including cross-coupling terms. It is clear that Pride and Berryman (2003a) formulated these equations in terms of field variables ${\varvec{\sigma }}$, $\mathbf{v}$, $\mathbf{q}_1$ and $\mathbf{q}_2$, $p_{\mathrm{f}1}$ and $p_{\mathrm{f}2}$. Nevertheless, it is inadequate and inconvenient to express the wave equations in terms of ${\varvec{\sigma }}$, and it is known from linear elastodynamics that these equations are expected to be formulated in terms of displacement $\mathbf{u}$. By contrast, in the quasi-static regime, it is adequate and convenient to express the governing equations for plane strain problems in terms of ${\varvec{\sigma }}$ (see Rice and Cleary 1976). In what follows, we will demonstrate that the governing equations of Pride and Berryman (2003a) for double-porosity, dual-permeability materials can be expressed in terms of displacement $\mathbf{u}$ and pore pressures $p_{\mathrm{f}1}$, $p_{\mathrm{f}2}$.

To show this, we first introduce the fluid mass conservation equations for the two phases, respectively:

$$\begin{aligned} -i\omega \zeta _1 +\nabla \cdot \mathbf{q}_1= & {} i\omega \zeta _{\mathrm{int}}, \end{aligned}$$

(85)

$$\begin{aligned} -i\omega \zeta _2 +\nabla \cdot \mathbf{q}_2= & {} -i\omega \zeta _{\mathrm{int}}, \end{aligned}$$

(86)

where $-i\omega \zeta _{\mathrm{int}}$ is the average rate at which fluid volume is being transferred from matrix phase into joint phase (the dimensional increment $\zeta _{\mathrm{int}}$ represents the “mesoscopic flow”) and defined as

$$\begin{aligned} -i\omega \zeta _{\mathrm{int}} ={\gamma }\left( \omega \right) \left( {p_{\mathrm{f}1} -p_{\mathrm{f}2} } \right) . \end{aligned}$$

(87)

In the above equation, ${\gamma }\left( \omega \right)$ is the transport coefficient which is determined for low and high frequencies. Following the approach of Johnson et al. (1987); Johnson 2001), Pride and Berryman (2003b) have modeled the transport coefficient in terms of

$$\begin{aligned} {\gamma }\left( \omega \right) ={\gamma }_\mathrm{m} \sqrt{1-i\frac{\omega }{\omega _m }}, \end{aligned}$$

(88)

where ${\gamma }_m$ and $\omega _m$ are parameters dependent on the constituent properties and the particular mesoscopic geometry. For the case of saturated rocks, the characteristic frequency is given by

$$\begin{aligned} \omega _m =\frac{\eta B_1 K_1 }{\kappa _1 \alpha _1 }\left( {{\gamma }_m \frac{V}{S}} \right) ^{2}\left( {1+\sqrt{\frac{\kappa _1 B_2 K_2 \alpha _1 }{\kappa _2 B_1 K_1 \alpha _2 }}} \right) ^{2}, \end{aligned}$$

(89)

with

$$\begin{aligned} {\gamma }_m =\frac{v_1 \kappa _1 }{\eta L_1^2 }. \end{aligned}$$

(90)

The length V / S and $L_1$ are, respectively, the volume-to-surface ratio and the average distance over which the fluid pressure gradient still exists in the final stages of equilibration, and, for idealized geometries, they can be analytically estimated (see Pride and Berryman 2003b).

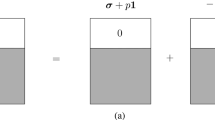
Next, expressing the constitutive relations (21) for the case of nonprincipal coordinates, we obtain

$$\begin{aligned} {\varvec{\sigma }}= & {} \left[ {\left( {b_{11} -2/{3\mu }} \right) e-b_{12} p_{\mathrm{f}1} -b_{13} p_{\mathrm{f}2} } \right] \mathbf{I}+2\mu {{\varvec{\varepsilon }}} \end{aligned}$$

(91)

$$\begin{aligned} \nabla \cdot \mathbf{q}_1= & {} i\omega \left[ {b_{12} e+\left( {b_{22} -\frac{{\gamma }}{i\omega }} \right) p_{\mathrm{f}1} -\left( {b_{23} -\frac{{\gamma }}{i\omega }} \right) p_{\mathrm{f}2} } \right] \end{aligned}$$

(92)

$$\begin{aligned} \nabla \cdot \mathbf{q}_2= & {} i\omega \left[ {b_{13} e-\left( {b_{23} -\frac{{\gamma }}{i\omega }} \right) p_{\mathrm{f}1} +\left( {b_{33} -\frac{{\gamma }}{i\omega }} \right) p_{\mathrm{f}2} } \right] \end{aligned}$$

(93)

after substituting for $\zeta _1$ and $\zeta _2$ using (85)–(87).

After that, applying the divergence operation to Eq. (83) yields

$$\begin{aligned} \left( {{\begin{array}{c} {\nabla \cdot \mathbf{q}_1 } \\ {\nabla \cdot \mathbf{q}_2 } \\ \end{array} }} \right) =-\frac{1}{\eta }\left( {{\begin{array}{c@{\quad }c} {\kappa _{11} }&{} {\kappa _{12} } \\ {\kappa _{12} }&{} {\kappa _{22} } \\ \end{array} }} \right) \left( {{\begin{array}{c} {\nabla ^{2}p_{\mathrm{f}1} -\omega ^{2}\rho _\mathrm{f} \nabla \cdot \mathbf{u}} \\ {\nabla ^{2}p_{\mathrm{f}2} -\omega ^{2}\rho _\mathrm{f} \nabla \cdot \mathbf{u}} \\ \end{array} }} \right) , \end{aligned}$$

(94)

Finally, substituting (83) and (91) into (82) and (92), (93) into (94), respectively, we can thus express the double-porosity governing equations of Pride and Berryman (2003a) in terms of $u_i$, $p_{\mathrm{f}1}$ and $p_{\mathrm{f}2}$:

$$\begin{aligned}&\mu \nabla ^{2}{} \mathbf{u}+\left( {b_{11} +\mu /3} \right) \nabla \nabla \cdot \mathbf{u}+\omega ^{2}\left[ {\rho +{i\omega \rho _\mathrm{f}^2 \left( {\kappa _{11} +2\kappa _{12} +\kappa _{22} } \right) }/\eta } \right] \mathbf{u}\nonumber \\&\quad -\left[ {b_{12} +{i\omega \rho _\mathrm{f} \left( {\kappa _{11} +\kappa _{12} } \right) }/\eta } \right] \nabla p_{\mathrm{f}1} -\left[ {b_{13} +{i\omega \rho _\mathrm{f} \left( {\kappa _{12} +\kappa _{22} } \right) }/\eta } \right] \nabla p_{\mathrm{f}2} =\mathbf{0}, \end{aligned}$$

(95)

$$\begin{aligned}&\frac{\kappa _{11} }{\eta }\nabla ^{2}p_{\mathrm{f}1} +\frac{\kappa _{12} }{\eta }\nabla ^{2}p_{\mathrm{f}2} +i\omega \left( {b_{22} -\frac{\gamma }{i\omega }} \right) p_{\mathrm{f}1} -i\omega \left( {b_{23} -\frac{\gamma }{i\omega }} \right) p_{\mathrm{f}2}\nonumber \\&\quad -\left( {\omega ^{2}\rho _\mathrm{f} \frac{\kappa _{11} +\kappa _{12} }{\eta }-i\omega b_{12} } \right) \nabla \cdot \mathbf{u}=0, \end{aligned}$$

(96)

$$\begin{aligned}&\frac{\kappa _{22} }{\eta }\nabla ^{2}p_{\mathrm{f}2} +\frac{\kappa _{12} }{\eta }\nabla ^{2}p_{\mathrm{f}1} +i\omega \left( {b_{33} -\frac{\gamma }{i\omega }} \right) p_{\mathrm{f}2} -i\omega \left( {b_{23} -\frac{\gamma }{i\omega }} \right) p_{\mathrm{f}1}\nonumber \\&\quad -\left( {\omega ^{2}\rho _\mathrm{f} \frac{\kappa _{12} +\kappa _{22} }{\eta }-i\omega b_{13} } \right) \nabla \cdot \mathbf{u}=0, \end{aligned}$$

(97)

where we have made use of the strain–displacement relations

$$\begin{aligned} e= & {} \nabla \cdot \mathbf{u}, \end{aligned}$$

(98)

$$\begin{aligned} {{\varvec{\varepsilon }} }= & {} \frac{1}{2}\left[ {\nabla \mathbf{u}+\left( {\nabla \mathbf{u}} \right) ^\mathrm{T}} \right] . \end{aligned}$$

(99)

Equation (95) is the dynamic equilibrium equation for two-phase mixtures, and Eqs. (96) and (97) are equilibrium equations for pore fluid in the matrix and joint phases, respectively, which allow for fluid cross-coupling between the phases. Berryman and Wang (2000) have pointed out that for wave propagation problems it is often adequate to assume that the cross-coupling term $\kappa _{12}$ vanishes as this effect is more important for long-term drainage of fluid than it is for short-term propagation of waves. If it is assumed that $\kappa _{12} =0$, Eqs. (95)–(97) will be simplified considerably and thus make the subsequent analysis somewhat less tedious.

If the joint phase is entirely embedded in the matrix phase (the corresponding condition satisfied in this case is $\nabla \cdot \mathbf{q}_2 =0)$, Pride and Berryman (2003a) suggested that the double-porosity theory can be reduced to the single-porosity Biot theory but with complex effective poroelastic moduli. By following their approach, these complex coefficients can also be determined as, in terms of $b_{ij}$

$$\begin{aligned}&\displaystyle K^\mathrm{eff}=b_{11} +\frac{b_{13}^2 }{b_{33} -{\gamma }/{i\omega }}, \end{aligned}$$

(100)

$$\begin{aligned}&\displaystyle \alpha ^\mathrm{eff}=b_{12} +\frac{b_{13} \left( {b_{23} -{\gamma }/{i\omega }} \right) }{b_{33} -{\gamma }/{i\omega }}, \end{aligned}$$

(101)

$$\begin{aligned}&\displaystyle B^\mathrm{eff}=\frac{\alpha ^\mathrm{eff}}{\left( {\alpha ^\mathrm{eff}} \right) ^{2}+K^\mathrm{eff}\left[ {\left( {b_{22} -{\gamma }/{i\omega }} \right) -{\left( {b_{23} -{\gamma }/{i\omega }} \right) ^{2}}/{\left( {b_{33} -{\gamma }/{i\omega }} \right) }} \right] }, \end{aligned}$$

(102)

where $K^\mathrm{eff}$ is the effective drained bulk modulus of the double-porosity materials, $\alpha ^\mathrm{eff}$ is the effective Biot–Willis constant, and $B^\mathrm{eff}$ is the effective Skempton’s coefficient. The effective undrained bulk modulus can then be determined by

$$\begin{aligned} K_\mathrm{u}^\mathrm{eff} =\frac{K^\mathrm{eff}}{1-\alpha ^\mathrm{eff}B^\mathrm{eff}}. \end{aligned}$$

(103)

In addition, they suggested that the permeability $\kappa$ of the effective Biot theory can be approximated by a simple harmonic mean of the two phases, that is

$$\begin{aligned} \frac{1}{\kappa }{=}\frac{v_1 }{\kappa _1}+\frac{v_2 }{\kappa _2 }. \end{aligned}$$

(104)

More generally, we might have to deal with the double-porosity governing equations directly to investigate associated wave phenomena in that media. By the way, it is impossible to apply their effective Biot theory to the study of wave phenomena associated with the second slow wave (which has been reported by Berryman and Wang 2000) in the double-porosity materials. Although the mathematical operations involved are more tedious than that for the single-porosity Biot theory, by formulating governing equations in terms of displacement and pore pressures will make the issue less troublesome since the three vector equations (82) and (83) (in component forms, there are together nine equations) have been reduced to a vector equation (95), plus the other two scalar equations (96) and (97).

In passing, using Biot’s approach (Biot 1956a), Berryman and Wang (2000) have also derived the double-porosity governing equations. In their model, the fluid transfer between the two phases was neglected with the assumption of $-i\omega \zeta _{\mathrm{int}} =0$ in Eqs. (85) and (86).