Abstract
In the present article, we simulate Lake Karla, an important natural ecosystem under restoration in Greece, operating also as a reservoir. The lake trophic state is characterized as hypertrophic with the expected negative effects on biodiversity. The simulation of Lake Karla is a significant tool in terms of understanding, predicting and managing the ecosystem. We perform simulations using PCLake, a software package for shallow lakes, which provides a full set of parameters, modeling a wide range of physical, chemical and biological variables. The model is calibrated based on the time series of six variables for year 2012 and validated using data of years 2014–2015. We present the nutrient flow dynamics for year 2012 on a trimester basis, and investigate the interrelations of nutrient cycling and trophic state, through observed variables such as phycocyanin and chlorophyll-a concentrations, Carlson Trophic State Index and ratio of Dissolved Inorganic Nitrogen to Soluble Reactive Phosphorus.
Similar content being viewed by others
1 Introduction
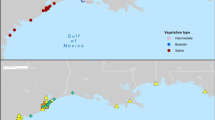
Lake Karla was the most important lake in the region of Thessaly and one of the largest lakes in Greece (Fig. 1). The lakeside villages depended mainly on the lake for their income, since their economy was based on fishing, boatbuilding and trading. In the winter of 1920–21, the lake reached the highest level ever (50 m above sea level). Its maximum depth gradually dropped from 5.5 m in 1940 to 2 m in 1950–51. The water level drop, the reduction of fish, the increase of salinity, the spreading of malaria due to the mosquitos, and the need for distribution of the lake’s land for agriculture were the reasons that lead authorities to the drainage of the lake (Nobile 1914; YPECHODE 1999; Zalidis et al. 2005; Jouni 2011). In few years time, it was generally perceived that the effects of lake drainage on the ecosystem and the economy were detrimental rather than beneficial, and the government decided to restore the lake with the construction of a reservoir, which started to operate in December of 2010. A historical overview of environmental policies that lead to the drainage of the lake has been presented by Laspidou and Gialis (2014).
The restored Lake Karla, which covers about one quarter of the surface of the original Lake, is located south of the Thessalian plain and borders the foothills of Mount Pelion and east–northeast of Mount Mavrovouni (Fig. 1). Lake Karla and the adjacent areas, Mavrovouni, Kefalovriso of Velestino and Neohori (GR1420004), are considered to be of high ecological importance and they are designated as a Natura 2000 site. The lake is now facing severe water quality and quantity problems. The water level, although fluctuating, is generally low, with inflows comprising mainly precipitation, surface runoff and inflow from Pinios River. To make things worse, a major mechanical failure in the pumping station has interrupted its operation for the last 3 years, resulting in no inflow from the river. Since the surrounding area is predominantly agricultural and is characterized by intense livestock activities, surface runoff that flows in the lake has high concentrations of nutrients (Laspidou and Samantzi 2014; Laspidou et al. 2011), resulting in the degradation of the lake trophic state, which is characterized as hyper-trophic (Papadimitriou et al. 2013) according to OECD and Carlson’s Trophic State Index (TSI) (Carlson 1977). Intense anthropogenic activities, lower precipitation rates and higher temperatures that have been recently observed due to climate warming trends have increased lake evaporation rates and have affected its quality and quantity; similar effects have been observed in other ecosystems as well (e.g., Wu et al. 2014; Jeppesen et al. 2015; Naselli- Flores and Barone 2003).
In this paper, we study the trophic conditions and water quality of Lake Karla and we explore the fate of nitrogen and phosphorus in the lake, by quantifying the material fluxes of all major forms of these nutrients through the use of the PCLake model. Therefore, we use ecological modeling in order to reveal the speciation of N and P in the lake, as well as the fluxes from one form to the other on a trimester basis, in order to capture their temporal variation.
2 Materials and Methods
2.1 Modeling Aspects: PCLake, a Shallow Lake Simulation Tool
PCLake is a model that describes a completely mixed water body; it includes the water column and the upper sediment layer of the bottom of the lake. It is mostly appropriate for modeling shallow, non-stratified lakes and can also take into account buffer zones. Mathematically, PCLake employs a number of coupled differential equations, one for each of the state variables included in the analysis. The structure of the model is schematically depicted in Fig. 2. All biota are modelled as functional groups. Other than the food web, PCLake also includes empirical or indirect relations between components, such as the effect of fish and macrophytes on the resuspension of sediment. All components are described in terms of dry weight (D), nitrogen (N) and phosphorus concentration (P). The mass balance of each component is dynamically checked during the calculations. Day is the uniform time unit for all processes; however, the relevant time scale for the output ranges from 1 week to 1 month (Janse and van Liere 1995).
PCLake model structure (lake part). “Shadowed” blocks denote compartments modelled in both dry weight and nutrient units. Three functional groups of phytoplankton are distinguished: cyanobacteria, diatoms and other small edible algae. Arrows with solid lines denote mass fluxes (e.g., food relations), arrows with dotted lines denote “empirical” relations (minus sign denotes negative influence otherwise positive influence). Egestion and mortality fluxes of animal groups and respiration fluxes are not shown (Janse and van Liere 1995)
The main inputs are: water inflow, infiltration or seepage, nutrient loading (N, P), particulate loading, temperature, daylight, lake fetch and depth, marsh zone proportion, sediment type and loading history. The outputs are biomass and concentrations of all variables. PCLake was initially constructed in order to model shallow lakes in the North European temperate climate. Therefore, it is not expected to capture the dynamics in Mediterranean lakes as well, due to the differences they have to the above. Mediterranean lakes are characterized by high temporal variability, usually enhanced by water level fluctuations (Coops et al. 2003) and are inhabited by fish species with different spawning frequencies, when compared to those in temperate lakes. Nevertheless, PCLake can sufficiently keep up with the trends of variables, such as chlorophyll-a (Chl-a), Secchi Depth (SD) and Carlson’s TSI, which is calculated based on Chl-a (Janse and van Liere 1995).
The model includes a series of abiotic and microbial processes, a phytoplankton module, an aquatic vegetation and wetland module, and a simplified food web. Each one of these modules is described by coupled differential equations, one for each state variable. The abiotic components taken into account are the inorganic matter (IM), humus, detritus, inorganic nutrients and Dissolved Oxygen (DO). The water level can be made variable depending on the inflow and outflow rates, which is crucial for capturing the water level fluctuations in Lake Karla. The sediment top layer retains a default thickness of 0.1 m and includes IM, humus, detritus and pore water. PCLake covers important indirect mechanisms that define the trophic state of a lake, such as the role of benthivorous fish and vegetation to resuspension. Nitrification of NH4 +, denitrification of NO3 −, exchange of dissolved P and N between pore water and water column and mineralization are modeled as well. Below, we present a series of representative basic equations for modeled variables in a descriptive format, to simplify presentation. A more detailed presentation of all equations modeled in PCLake is available in Janse (2005).
Phytoplankton is divided into three functional groups: diatoms, cyanobacteria and small edible algae, each described by the following equation (functional groups are denoted by x):
At the same time, nutrients N and P stored in phytoplankton (denoted by y) are described by the following equation:
Diatoms and cyanobacteria production is modeled based on the Steele’s equation (Di Toro and Matystik 1980). Other edible algae production is simulated using a Monod-type equation, assuming no light inhibition. The nutrient uptake rate depends on external nutrient concentration, with a maximum determined by the cell quota (Riegman and Mur 1984). The biomass production is given by the Droop (1974) equation.
Aquatic vegetation is modeled as one lumped group described by the following differential equations:
where, biomass is denoted by x. Nutrients N and P stored in aquatic plants are denoted by y and are described by the following equation:
The foodweb includes zooplankton, macrozoobenthos and fish, with each animal group (denoted by z) being described by the following general equation:
2.2 Lake Sampling Campaigns
Monthly water samples in three lake sampling stations for Chl-a and physical-chemical parameters such as nutrients, pH, DO, conductivity and SD were collected during 2012 as described in Chamoglou et al. (2014), so a total of 12 sampling campaigns were conducted. Specifically, nutrients, nitrate (NO3-N), ammonium (NH4-N) and Total Phosphorus (TP) in lake water were determined from water sample analyses according to Standard Methods (APHA 2005). Sampling procedures are described in more detail in Chamoglou et al. (2014). At the same time, lake water level was recorded on a monthly basis by the Lake Karla Management Body (www.fdkarlas.gr), allowing us to calculate the average monthly lake volume. Meteorological data, such as mean annual wind speed, mean monthly water temperature and precipitation were obtained from the University of Thessaly School of Agricultural Sciences meteorological station installed at the Experimental Field.
Monthly lake sampling campaigns were initiated again in March 2014 and were continued until March 2015, creating a second time series dataset for the 13-month period. Water samples for nutrients, Chl- a and phycocyanin were collected during that period. Samples were taken from the upper 50 cm of the water column at five representative sampling stations. Station 1 (ST1) is located at the north-east of a gravity flow inlet at the southern end of the lake. Station 2 (ST2) is located on the south-east shore of Lake Karla and it is characterized by heavy cyanobacterial blooms in warm months. Station 3 (ST3) is located on the north-east shore of Lake Karla and was selected to represent conditions of the lake that are exposed to runoff coming from livestock grazing, animal sheds and mountainous land from the eastern part of Lake Karla catchment. Station 4 (ST4) is close to the rock-covered embankment by the pumping station inlet. Station 5 (ST5) is a pelagic station located near the center of the lake. A map of all sampling stations described here is shown in Fig. 1.
Temperature, pH, D.O. and conductivity were measured in situ by electrode probes (YSI, USA). Concentrations of nitrate \( \left(N{O}_3^{-}\right) \), ammonium \( \left(N{H}_4^{+}\right) \) and TP in lake water were determined from water sample analyses according to Standard Methods (APHA 2005). Water transparency, expressed as SD, was measured with a Secchi Disk. The content of the algal biomass in water samples was estimated by Ch-a and the content of the cyanobacterial biomass in water samples was estimated by Phycocyanin. Chl-a was extracted with 95 % acetone after filtration of samples on GF/F filters (0.45 μm, 47 mm) and measured spectrophotometrically at wavelengths of 750, 664, 647, 630, 510 and 480 nm (APHA 2005). For the determination of phycocyanin, samples were filtered through GF/F filters (0.22 μm, 47 mm). Phycocyanin was extracted by repeated freezing and thawing of cells in 10 mM phosphate buffer pH 7. The extract was centrifuged at 40,000 g for 1 h and supernatant was used for the determination of phycocyanin concentrations, by measuring the fluorescence of phycocyanin at an excitation wavelength of 620 nm and an emission wavelength of 645 nm. Fluorescence was measured by a fluorescence spectrometer.
2.3 Input, Calibration and Validation of the Model
The lake ecosystem is calibrated using the dataset obtained in year 2012. The input inserted into the model is extensive, so we list here a few major variables: lake hydrological and meteorological conditions, its dimensions and geometry for the calculation of the fetch, soil type for lake sediments, nutrient loadings, etc. Inputs can be either constant values, or time series, depending on data availability and the nature of each variable. Most of the aforementioned variables are inserted as time series.
Inputs and initial values used in PCLake for both the calibration and validation processes are presented in Table 1. PCLake, if run for a sufficiently long time, has the capacity to reach a steady state that is independent of the initial condition; in other words, even if the initial values used are not precise enough, the model outcome should be the same. Following this reasoning, we used measured data whenever possible and assumed values when data were not available. Specifically, initial values for piscivorous fish were assumed to be zero for both calibration and validation steps; this assumption was based on a combination of findings from the literature and actual observations: The top-down control mechanism is not followed in warmer lakes as a result of different population dynamics. In warm lakes, piscivorous fish are less likely to prevail than omnivorous and benthivorous (Fernando 1994), which in addition to the low pressure on them due to the absence of the piscivorous fish, have frequent births throughout the year (Beklioglu et al. 2007). This lack of top-down control mechanism results in very low zooplankton concentrations, which in turn, results in high phytoplankton concentrations (Fernando 1994). Also, since there are no submerged or upmerged macrophytes in the lake, we set the initial value of macrophytes to zero in the model. Finally, water inflow values for the validation period appear to be lower than the ones used for the calibration period; this is true since the former includes precipitation and smaller inflows from streams collecting water from the lake catchment area, but no inflows from Pinios river (interrupted due to a pump failure), while the latter includes inflows from Pinios as well. Evaporation was estimated using the Thornthwaite method (Thornthwaite 1948), while infiltration was provided to us by the Lake Karla Management Body.
The model is calibrated through successive trials of seven-parameter combination runs; the parameters were obtained by Janse (2005) who provides a Table with the rankings of PCLake parameters and input factors according to sensitivity. Each parameter is listed to mostly influence a specific variable; i.e., for each variable, such as Chl-a, SD, TP, etc., a different list of parameters that the variable is expected to be sensitive to is provided. We picked a list of seven most influential parameters, by ensuring that they affect the following four variables the most: Chl-a, SD, TP and Total Nitrogen. The parameters, mostly relevant to our system and our available data, are the following: maximum filtering rate, diatom maximum growth rate, greens maximum growth rate, vegetation maximum growth rate, selection factor for greens, maximum sedimentation velocity of detritus and fraction for vegetation surviving in winter. The calibration is based on monthly time series sets of six variables, the concentration of ammonium ions \( \left(N{H}_4^{+}\right) \), concentration of nitrate ions \( \left(N{O}_3^{-}\right) \), concentration of DO, transparency through SD, concentration of Chl-a and concentration of phosphate ions \( \left(P{O}_4^{3-}\right) \). For every measurement, the difference between measured and simulated values is calculated and then used to compute the sum of squares for each variable. The model is calibrated for maximum Posterior Density, according to the following:
where, var refers to each one of the six aforementioned variables, nvar is the number of measurements for each variable and the Sum of Squares var is calculated as shown in Eq. 11.
where, obs var,t is the observed value of the variable in time t and \( {model}_{var,t} \) is the simulated value of the variable in time t.
The six obtained sum-of-squares values are used to calculate the marginal posterior density:
In order to adjust the model output to the observed values of the six variables, trials of different combinations of the seven parameters were conducted. The criterion with which the calibration is held out is the maximization of the Posterior Density function.
Next, we proceeded with the validation of the model. We used an independent dataset, i.e., the one that we obtained from the sampling campaigns during the period March 2014 to March 2015 to conduct model validation, which was based on monthly time series sets of six variables, the concentration of ammonium ions \( \left(N{H}_4^{+}\right) \), concentration of nitrate ions \( \left(N{O}_3^{-}\right) \), concentration of DO, transparency through SD, concentration of Chl-a and concentration of TP. Calibration and validation results are presented for Carlson’s TSI, which is a useful quantity for the assessment of the trophic state of the Lake.
To quantify the prediction errors, several standard accuracy measures were used such as the Root Mean Squared Error (RMSE), Mean Error (ME), Mean Absolute Percentage Error (MAPE) and Mean Absolute Error (MAE). To evaluate the goodness of the fit and suitability of the model, the R-square criterion was also used.
3 Results and Discussion
3.1 Model Calibration and Validation
We followed the calibration and validation procedures described above and obtained satisfactory results regarding the level of agreement of simulated and observed values. In Fig. 3, we present the Chl-a based Carlson’s TSI as predicted by the model, along with observed values from the Lake Karla sampling campaigns. Goodness of fit is assessed via the statistical analysis performed (shown in Table 2). We can see that the fit is very good for the calibration dataset, while it appears to be adequate for the validation step; this enforces the argument that PCLake can be used for modeling the trophic state of shallow Mediterranean lakes.
3.2 Simulation of Nutrient Flows for Year 2012
The flow of materials and energy in a lake is of great interest, since they can be very helpful in revealing the basis on which the lake responds to external loadings. Understanding those lake mechanisms, as well as the interactions between lake components through ecosystem modeling is a powerful tool that helps us reveal and quantify the major internal processes and pathways. The fate and transport of nutrient loads, following their delivery into a lake, result from the integration of all hydrologic, physical, chemical, and biological processes that operate within that lake. The power of PCLake is that it includes, characterizes and quantifies all these complex processes and can provide predictions for these quantities that may have been difficult to foresee before hand.
Modeling nitrogen dynamics in our system means that we need to take into account hydrology, primary productivity, sediments and nitrogen speciation. In this work, we show flows within the lake for two types of nitrogen species: nitrate (\( N{O}_3^{-} \)) and ammonium (\( N{H}_4^{+} \)). Nitrates—a dissolved species—can flow in the lake through external loadings, mainly from fertilizers and livestock breeding activities; part of it is assimilated in algae—which includes blue-green and green algae and diatoms—through primary production. It should be noted here that there are no macrophytes in the lake, due to the fact that the lake is in a highly turbid state. Nitrates can exit the water column, to enter the sediments and/or groundwater through the process of infiltration, while, under anaerobic conditions, it can get lost to the atmosphere as molecular nitrogen (N 2 ) through the process of denitrification. Sediment resuspension and diffusion can recycle nitrates back to the water column (Laspidou and Vaina 2009), while nitrification converts ammonium to nitrates when plenty of oxygen is present and when temperature is within the optimal range of 27 to 32 °C, through the process of nitrification. The reaction slows down as we move away from the optimal temperature range. This nitrate cycling and transformation in Lake Karla is shown in Fig. 4 for all four seasons of the year 2012. All inflows are reported as percentages of the total annual nitrate inflow; thus, all four values add up to 100 %. We see that the highest inflow is observed in the summer (35 %), which is expected due to the intensity of agricultural activities during this trimester. Greece is a warm Mediterranean country, so agriculture starts early in the spring and continues until late autumn, with farmers choosing different crops throughout most of the year. Furthermore, nitrogen compounds are transferred through agricultural run-off, which is more intense when it is followed by rainy events. In Greece, although annual average precipitation is relatively low compared to that of North Europe and unequally distributed throughout the year, 35 % or more of the annual precipitation corresponds to the warm 6-month period (Di Castri and Mooney 1973). For this reason, there is a significant inflow of nitrates during spring and autumn (27 and 26 %, respectively), while the inflow is the highest during the summer (35 %) and the lowest during the winter (12 %). The flows reported in the Figure, are fractions of the incoming nitrates, which are different for each trimester.
In Fig. 4, we see that primary productivity has percentages much higher than 100 %, which is justified because of extensive internal cycling in the lake. The lake is hypertrophic with thick algal blooms almost reaching a “mat” stage especially in the summer and autumn when temperatures and solar radiation remain high (Papadimitriou et al. 2013; Chamoglou et al. 2014); therefore, we see that a large percentage of nitrates goes to primary production. Nitrification is also high throughout the year, while it only drops during the winter when temperatures are relatively low. This is also supported from the data, showing Chl-a concentrations much higher during the warm months than winter values (Chamoglou et al. 2014). Due to the lake low water level, water temperatures change relatively quickly and adjust close to air temperatures.
There is evidence in the literature that the magnitude of the N:P ratio is an important factor that controls the growth of cyanobacteria (Bulgakov and Levich 1999). In order to assess the significance of this ratio and the role it plays in Lake Karla, and to check the validity of the nitrate fluxes produced by PCLake (Fig. 4), we use the phycocyanin measurements. Phycocyanin is more accurate and useful than Chl-a in quantitatively measuring cyanobacterial blooms (Ahn et al. 2002). For this purpose, we present in Fig. 5 a comparative diagram of dissolved inorganic nitrogen to soluble reactive phosphorus (DIN:SRP) to phycocyanin and Chl-a concentrations, showing that once the ratio declines and reaches values of N:P equal to or less than 10, excessive growth of cyanobacteria takes place. This is observed in May, as shown in the Figure. When the ratio reaches values greater than 10 (observed in August), cyanobacteria growth stops and concentrations eventually decline to winter levels. This is in accordance with our modeling results showed in Fig. 4, in which we see that the highest percentage of nitrate flows towards blue-green production in the summer (0.35 of yearly input × 233 % = 81.6 % in the summer vs. 0.12 of yearly input × 69 % = 8.28 % in the winter). Similar results are presented by Bulgakov and Levich (1999), who showed that the critical N:P mass ratios at which cyanobacteria (both N2-fixing and non- N2-fixing) tend to dominate in lakes are found to fluctuate between 5 and 10. Dominance of cyanobacteria in Lake Karla is also supported in the same diagram, which shows that concentrations of phycocyanin are much higher than concentrations of Chl-a, mainly during the warm months. Papadimitriou et al. (2013) also showed that cyanobacteria consisted on average ca. 75 % of the total phytoplankton biomass found in Lake Karla and furthermore phytoplankton blooms were formed exclusively by cyanobacteria from June to September.
Nitrification seems to be hindered by low temperatures in the winter; thus, it is lower compared to the other seasons. DO is also high throughout the year, since the lake is very shallow and has no thermal stratification. Compared to deep lakes that present an anoxic hypolimnion during stratification, shallow lakes are usually well-mixed and oxidized throughout the water column (Søndergaard et al. 2003). DO solubility decreases with temperature and lake thermal stratification would create a corresponding DO concentration profile with depth, something that is not observed here (Bella 1970). Furthermore, algal blooms produce significant quantities of oxygen through photosynthesis, so it appears that the lake is not limited by oxygen for nitrification. Another consequence of this is that we did not observe any anoxic zones in the lake; thus, denitrification appears very low throughout the year. Even in oxidized shallow lakes, we usually see some denitrification, which is expected to take place in the sediments, or even in the water column, when DO concentration may occasionally drop (Janse 2005; Messer and Brezonik 1983). Resuspension and infiltration, as provided by the PCLake model, are relatively low when compared to the rest of the fluxes, while diffusion from the sediments seems to be significant (Laspidou and Vaina 2009). The newly-restored Lake Karla was used as agricultural land in the past, so large quantities of nutrients are expected to be trapped in the sediments and are expected to leach to the water column throughout the year.
In Fig. 6, we illustrate the seasonal inflow of \( N{H}_4^{+} \) as wells as its pathways in the system, as provided by the PCLake model. Ammonium is assimilated in biomass through primary production, while part of it is also converted to nitrates through the process of nitrification, when oxygen is present. As with nitrates, a small part of ammonium is lost through infiltration in the sediments. Part of the ammonia that is incorporrated in the biomass of fish and zooplankton is returned back to the water column through excretion/egestion/mortality, while detritus converts dead organic matter to ammonium through mineralization. Finally, sediment resuspension and diffusion also returns part of soluble ammonium back to the water column.
As with nitrates shown in Fig. 4, all external inflows are reported as percentages of the annual inflow of \( N{H}_4^{+} \) in the lake. We see that the pattern of seasonal variability of ammonia inflow is very similar to that of nitrates following the same reasoning, as it was simulated for year 2012. Primary production is still a large flow of ammonium in the lake, while nitrification in Fig. 6 is exactly the same as in Fig. 4 (although the absolute values are the same, the reported values shown in the Figures do not match, since they are percentages of total annual inflow). Internal cycling appears strong here too, with zooplankton and fish returning significant quantities of nitrogen back in the water in the form of ammonium (Stampouli et al. 2012). Detritus also mineralizes a significant amount of ammonium, enhancing internal cycling. Diffusion from the sediments follows the same pattern as with nitrates and is relatively high, as expected.
In Fig. 7, we illustrate the seasonal inflow of \( P{O}_4^{3-} \) as well as its pathways in the system similarly to Figs. 4 and 6. Phosphate ions are assimilated in biomass through primary production. As with nitrates and ammonium, a small part of phosphates is lost through infiltration in the sediments, via the seepage of interstitial phosphates. Similarly to ammonium, part of the phosphorus that is incorporrated in the biomass of fish and zooplankton is returned back to the water column through excretion/egestion/mortality, while detritus converts dead organic matter to phosphates through mineralization. Finally, sediment resuspension and diffusion also returns part of soluble phosphates back to the water column, while the same is true for the desorption of phosphates from inorganic matter, where it is bound. In Fig. 7, we see that diffusion of phosphates out of the sediments is the highest in the summer (0.34 × 155 % = 52.7 % in the summer). This is in accordance with previous studies on Lake Karla (Jouni 2011), noting that increased phosphorus release from sediment is expected during summer, not because of changing amounts of external input, but because of the interaction between the sediments and the overlying water column. According to Caraco et al. (1990), phosphate mobilization from sediments is more intense in brackish than in freshwater systems. Lake Karla can be characterized as a brackish water ecosystem with high conductivity levels (measured conductivity levels range from 2 to 3.7 mS/cm); high evaporation rates in the summer time result in increased conductivities intensifying phosphate release from sediments in the water column.
4 Conclusions
In this paper, we simulated a shallow hypertrophic Mediterranean lake, Lake Karla, using the PClake model in order to reveal and quantify the nutrient fluxes in the lake. The PCLake model is designed for Northern European temperate lakes, rather than Mediterranean lakes; however, after careful calibration and validation of the model, we can conclude that PClake can adequately simulate Lake Karla as an ecosystem. Nutrient flows are an essential element in order to understand and quantify the inlake processes and pathways, and thus, foresee all the possible effects of the external nutrient loadings to the ecosystem. PCLake can simulate all these fluxes, while it provides detailed information about the fate of nutrients in the lake and can be a powerful tool in order to manage the system effectively in the direction of its remediation.
References
Ahn CY, Chung AS, Oh HM (2002) Rainfall, phycocyanin, and N:P ratios related to cyanobacterial blooms in a Korean large reservoir. Hydrobiologia 474:117–124
APHA (2005) Handbook, of standard methods for the examination of water and wastewater, 21st edn. Published jointly by American Public Health Association, American Water Works Association, and Water Environment Federation
Beklioglu M, Romo S, Kagalou I, Quintana X, Bécares E (2007) State of the art in the functioning of shallow Mediterranean lakes: workshop conclusions. Hydrobiologia 584:317–326
Bella DA (1970) Dissolved oxygen variations in stratified lakes. J Sanit Eng Div 96(5):1129–1146
Bulgakov NG, Levich AP (1999) The nitrogen:phosphorus ratio as a factor regulating phytoplankton community structure. Arch Hydrobiol 146:3–22
Caraco N, Cole J, Likens GE (1990) A comparison of phosphorus immobilization in sediments of freshwater and coastal marine systems. Biogeochemistry 9:277–290
Carlson RE (1977) A trophic state index for lakes. Limnol Oceanogr 22(2):361–369
Chamoglou M, Papadimitriou T, Kagalou I (2014) Key-descriptors for the functioning of a Mediterranean reservoir: the case of the New lake Karla-Greece. Environ Process 1:127–135
Coops H, Beklioglu M, Crisman TL (2003) The role of water-level fluctuations in shallow lake ecosystems—workshop conclusions. Hydrobiologia 506(1–3):23–27
Di Castri F, Mooney HA (eds) (1973) Mediterranean type ecosystems: origin and structure. Springer, New York, 405 pp
Di Toro DM, Matystik WF (1980) Mathematical models of water quality in large lakes. Part 1: Lake Huron and Saginaw Bay. EPA 600/3-80-56, Duluth, MI, USA
Droop MR (1974) The nutrient status of algal cells in continuous culture. J Mar Biol Assoc UK 54:825–855
Fernando CH (1994) Zooplankton, fish and fisheries in tropical freshwaters. Hydrobiologia 272:105–123
Janse J H (2005) Model studies on the eutrophication of shallow lakes and ditches. PhD thesis, Wageningen University
Janse JH, Van Liere L (1995) PCLake - a modelling tool for the evaluation of lake restoration scenarios. Water Sci Technol 31:371–374
Jeppesen E, Brucet S, Naselli-Flores L, Papastergiadou E, Stefanidis K, Nõges T, Nõges P, Attayde JL, Zohary T, Coppens J, Bucak T, Menezes RF, Freitas FRS, Kernan M, Søndergaard M, Beklioğlu M (2015) Ecological impacts of global warming and water abstraction on lakes and reservoirs due to changes in water level and related changes in salinity. Hydrobiologia 750:201–227
Jouni S (2011) Current trophic status of lake Karla, Greece and proposals for remediation. M.Sc. Thesis, University of Edinburgh, UK
Laspidou CS, Gialis S (2014) Lake Karla and the contradictory character of Greek environmental policies: a brief historical overview. Proceedings to the IWA Regional Symposium on Water, Wastewater and Environment: Traditions and Culture, 22–24 March 2014, Patras, Greece
Laspidou CS, Samantzi V (2014) Identifying and quantifying nitrogen and phosphorus loadings from agriculture and livestock waste in the Penios River Basin District. Toxicol Environ Chem 97(1):90–102
Laspidou CS, Vaina V (2009) Ecosystem modeling of sediment dynamics in the constructed wetland Carla in Central Greece. Int J Des Nat Ecodyn 3(4):273–280
Laspidou C, Kakoulidis I, Loukas A (2011) Ecosystem simulation modeling of nitrogen dynamics in the restored lake Karla in Greece. Desalin Water Treat 33:1–3
Messer J, Brezonik PL (1983) Comparison of denitrification rate estimation techniques in a large, shallow lake. Water Res 17:631–640
Naselli- Flores L, Barone R (2003) Steady- state assemblages in a Mediterranean hypertrophic reservoir. The role of microcystis ecomorphological variability in maintaining an apparent equilibrium. Hydrobiologia 502:133–143
Nobile I (1914) Thessaly’s flood-protection Systems. Greek Ministry of Transport, Athens
Papadimitriou T, Katsiapi M, Kormas KA, Moustaka-Gouni M, Kagalou I (2013) Artificially-born “killer” lake: phytoplankton based water quality and microcystin affected fish in a reconstructed lake. Sci Total Environ 452–453:116–124
Riegman R, Mur LR (1984) Theoretical considerations on growth kinetics and physiological adaptation of nutrient-limited phytoplankton. Arch Microbiol 140:96–100
Søndergaard M, Jensen JP, Jeppesen E (2003) Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 506–509:135–145
Stampouli Z, Papadimitriou T, Kagalou I (2012) Evaluation of the ecological state of the “New” Lake Karla, Thessaly with emphasis on the zooplankton community, Proceedings of the 34th Scientific Conference of Hellenic Association for Biological Sciences Trikala May 17–19, 2012
Thornthwaite CW (1948) An approach toward a radiation classification of climate. Geogr Rev 38(1):55–94
Wu J, Liu W, Zeng H, Ma L, Bai R (2014) Water quantity and quality of Six lakes in the arid Xinjiang Region, NW China. Environ Process 1:115–125
YPEHODE: Greek Ministry of Environment, Regional Planning and Public Works (1999) “Lake Karla Restoration”, Environmental Technical report, Cost-Benefit Study and Supportive Studies (in Greek)
Zalidis G, Takavakoglo V, Panoras A, Bilas G, Katsavouni S (2005) Reestablishing a sustainable wetland for former Lake Karla, Greece, using Ramsar Restoration guidelines. Environ Manag 34:875–886
Acknowledgments
This research was conducted in the framework of the project LAKEREMAKE, which is implemented under the “ARISTEIA II” Action of the Operational Programme “Education and Lifelong Learning” and is co-funded by the European Social Fund (ESF) and National Resources. An initial version of this paper has been presented in the 12th International Conference on Protection and Restoration of the Environment, Skiathos Island, Greece, June 29 to July 3, 2014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mellios, N., Kofinas, D., Laspidou, C. et al. Mathematical Modeling of Trophic State and Nutrient Flows of Lake Karla using the PCLake Model. Environ. Process. 2 (Suppl 1), 85–100 (2015). https://doi.org/10.1007/s40710-015-0098-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40710-015-0098-y