Abstract
In our previous work (Shen et al 2020 Metrologia 57 025015; Booth et al 2019 New J. Phys. 21 102001), we have reported the first primary quantum pressure standard based on the loss rate of cold rubidium atoms from a magnetic trap. We have shown that this standard is self-calibrating. That is, the single parameter required to quantify the pressure or particle flux impinging on the sensor atoms, 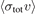 , can be determined experimentally. In this paper, we refine our procedure to extract the trap loss rate coefficient by expressing the measured trap loss rate of the rubidium atoms as a convolution of the universal loss rate expression from Shen et al (2020 Metrologia 57 025015) and Booth et al (2019 New J. Phys. 21 102001) with the energy distribution of the rubidium atoms in the trap. We report improved
, can be determined experimentally. In this paper, we refine our procedure to extract the trap loss rate coefficient by expressing the measured trap loss rate of the rubidium atoms as a convolution of the universal loss rate expression from Shen et al (2020 Metrologia 57 025015) and Booth et al (2019 New J. Phys. 21 102001) with the energy distribution of the rubidium atoms in the trap. We report improved 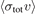 values for 87Rb–X (X = He, Ar, Xe, H2, N2, and CO2) collision pairs. All are systematically higher than our previously reported values, although the differences are less than 2%. The calibration factor of an ionization gauge for nitrogen obtained using the cold atom standard, ig = 0.950 (19), agrees with the value obtained by NIST, ig = 0.940 (26) calibrated against their orifice flow standard.
values for 87Rb–X (X = He, Ar, Xe, H2, N2, and CO2) collision pairs. All are systematically higher than our previously reported values, although the differences are less than 2%. The calibration factor of an ionization gauge for nitrogen obtained using the cold atom standard, ig = 0.950 (19), agrees with the value obtained by NIST, ig = 0.940 (26) calibrated against their orifice flow standard.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The idea of using cold atoms to measure the pressure in a vacuum was introduced in the 1980s [3], based on the observations that collisions between the trapped cold atoms and the background particles in the vacuum system limit the trapped ensemble lifetime. Since then, the trap loss rate of atoms has been used to provide an estimate of the pressure in the vacuum system [4–6], albeit with limited accuracy and precision. In 2011, it was proposed that an accurate primary pressure standard could be created by measuring the loss rate of atoms confined in a shallow trap whose depth, U, was well known [7, 8]. Namely, the trap loss rate, Γ(U), induced by collisions with room temperature background gas at density, n, can be described by,
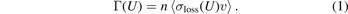
Here the loss rate coefficient, 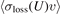 , is the trap depth dependent loss rate cross-section times the relative speed of the collision partners averaged over the Maxwell–Boltzmann (MB) speed distribution of the background particles at temperature, Troom. Following the proposal, vacuum measurements using cold atoms in different traps were demonstrated such as magnetic trap based measurements [9, 10], magneto-optical trap based measurements [11, 12], and optical dipole trap based measurements [13]. Although these prior studies showed the promise of realizing a primary cold atom pressure standard in the ultra-high vacuum (UHV, p < 10−6 Pa) regime, their results were limited by the lack of accurate knowledge of the loss rate coefficient,
, is the trap depth dependent loss rate cross-section times the relative speed of the collision partners averaged over the Maxwell–Boltzmann (MB) speed distribution of the background particles at temperature, Troom. Following the proposal, vacuum measurements using cold atoms in different traps were demonstrated such as magnetic trap based measurements [9, 10], magneto-optical trap based measurements [11, 12], and optical dipole trap based measurements [13]. Although these prior studies showed the promise of realizing a primary cold atom pressure standard in the ultra-high vacuum (UHV, p < 10−6 Pa) regime, their results were limited by the lack of accurate knowledge of the loss rate coefficient, 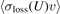 , and the trap depth, U.
, and the trap depth, U.
In our recent work [1, 2], we provided a way of measuring the values of the loss rate coefficients experimentally and used this technique to realize the first primary cold atomic pressure standard for the UHV. We have shown that the loss rate coefficient at small trap depths follows a universal scaling law,

In equation (2), the nature of the long-range interaction is encoded in the universal coefficients, βj . In [1, 2], we have presented these values for van der Waals interactions, −C6/R6 (other long-range interactions, −Cn /Rn , for n = 4, 5, etc constitute different universality classes with distinct coefficients). The characteristic energy scale, Ud, is the so-called quantum diffractive energy [6],
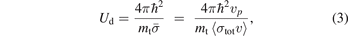
where mt is the mass of the trapped atom, 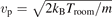 is the most probable velocity of the background particles of mass m at temperature Troom. Finally,
is the most probable velocity of the background particles of mass m at temperature Troom. Finally, 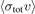 is the velocity averaged total collision cross-section coefficient. The quantum diffractive energy, Ud, varies from collision pair to collision pair and defines the energy scale below which quantum diffractive collisions dominate the variation of the loss rate with trap depth. This energy scale is dictated by the Heisenberg uncertainty principle. Initially, the trapped sensor atom has a small momentum and a large de Broglie wavelength. A collision localizes the sensor atom to a spatial region determined by the collision cross-section,
is the velocity averaged total collision cross-section coefficient. The quantum diffractive energy, Ud, varies from collision pair to collision pair and defines the energy scale below which quantum diffractive collisions dominate the variation of the loss rate with trap depth. This energy scale is dictated by the Heisenberg uncertainty principle. Initially, the trapped sensor atom has a small momentum and a large de Broglie wavelength. A collision localizes the sensor atom to a spatial region determined by the collision cross-section,  . Complementarity imposes a corresponding change in the atom's momentum distribution through the interaction potential. A collision that imparts little energy and momentum to the sensor atom is referred to as a quantum diffractive collision [14]. Measuring the trap loss rate versus trap depth for shallow magnetic traps reveals the spectrum of energies transferred to the trapped atoms by quantum diffractive collisions. In turn, this allows the sole experimental parameter,
. Complementarity imposes a corresponding change in the atom's momentum distribution through the interaction potential. A collision that imparts little energy and momentum to the sensor atom is referred to as a quantum diffractive collision [14]. Measuring the trap loss rate versus trap depth for shallow magnetic traps reveals the spectrum of energies transferred to the trapped atoms by quantum diffractive collisions. In turn, this allows the sole experimental parameter, 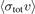 , to be extracted from a fit of the data to equation (2). In other words, this is a self-calibrating quantum pressure standard with no need of a priori knowledge of the interaction potentials nor computations of loss rate coefficients.
, to be extracted from a fit of the data to equation (2). In other words, this is a self-calibrating quantum pressure standard with no need of a priori knowledge of the interaction potentials nor computations of loss rate coefficients.
Using this self-calibrating pressure measurement method, we determined the values of 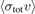 for collisions between Rb atoms and both atomic gas species (He, Ar and Xe) and molecular species (H2, N2, and CO2) [1, 2]. In this short communication, we further refine the
for collisions between Rb atoms and both atomic gas species (He, Ar and Xe) and molecular species (H2, N2, and CO2) [1, 2]. In this short communication, we further refine the 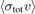 values by eliminating the systematic error introduced through the approximate expression previously used to compute the loss rate coefficients. In section 2, we start by re-stating the definition of the mean trap depth for an ensemble of trapped atoms. Then, the previously reported loss rate coefficients, calculated by substituting the mean trap depth into equation (2), are compared with the more rigorous computation which averages equation (2) over the trapped atom ensemble energy distribution. We then discuss the systematic error introduced in the determination of
values by eliminating the systematic error introduced through the approximate expression previously used to compute the loss rate coefficients. In section 2, we start by re-stating the definition of the mean trap depth for an ensemble of trapped atoms. Then, the previously reported loss rate coefficients, calculated by substituting the mean trap depth into equation (2), are compared with the more rigorous computation which averages equation (2) over the trapped atom ensemble energy distribution. We then discuss the systematic error introduced in the determination of 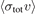 when the experimental data are fit to equation (2) using the previous, approximate expression for the loss rate coefficients compared to the more rigorous definition introduced in this work.
when the experimental data are fit to equation (2) using the previous, approximate expression for the loss rate coefficients compared to the more rigorous definition introduced in this work.
2. Refining the ensemble averaged loss rate coefficients
Central to the realization of a high precision self-calibrating quantum pressure standard is the requirement that the trap depth, U, be tunable to map out the loss rate coefficient as a function of the trap depth, as described by equation (2). To control the trap depths, the atoms in the magnetic trap are subjected to radio-frequency (RF) radiation whose frequency is swept between νmin and νmax. The RF field couples the hyperfine state |F, mF ⟩ to other adjacent hyperfine states |F, mF ± 1⟩. Atoms with energies greater than Emax = hνmin will encounter this resonant RF field and be transferred into an untrapped state. Thus, the RF field sets a precise and tunable Emax for atoms in the magnetic trap.
The trap depth for a trapped atom with energy, E, is defined as U = Emax − E. Therefore, the mean trap depth, 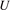 , of the sensor ensemble with energy below Emax is determined by averaging the trap depth of each atom, U, over the energy distribution of the selected ensemble,
, of the sensor ensemble with energy below Emax is determined by averaging the trap depth of each atom, U, over the energy distribution of the selected ensemble,
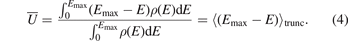
Here '⟨⟩trunc' indicates the ensemble average of the quantity in the bracket over the energy range, [0, Emax], truncated by the RF radiation. ρ(E) represents the energy distribution of the whole ensemble before applying any RF field and can be measured experimentally. It is found to be modeled very well by a MB distribution of a mean temperature, T, shifted by a fixed amount of energy, Emin (owing to a slight misalignment of the MOT and MT used in the measurements),
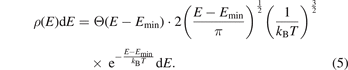
Θ(E − Emin) is the Heaviside function, which indicates that there are no atoms with energies below Emin in the MT, and the remaining factor is a regular MB distribution in energy above Emin.
As a first approximation used in [1, 2], we directly inserted the mean trap depth, 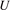 , into equation (2) to calculate the loss rate coefficient as expressed in the following,
, into equation (2) to calculate the loss rate coefficient as expressed in the following,
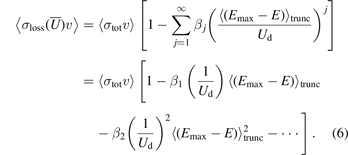
A more rigorous approach is to average the loss rate coefficient 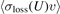 of an atom at finite trap depth, U, over the energy distribution of the selected ensemble,
of an atom at finite trap depth, U, over the energy distribution of the selected ensemble,
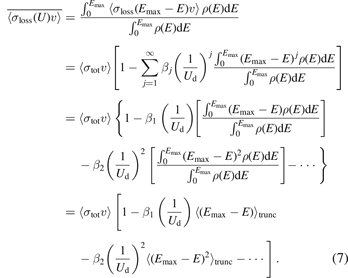
One observes that these two expressions of the loss rate coefficient deviate from each other. The approximate loss rate coefficient expression (equation (6)) replaces the jth moment 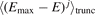 in each term of the polynomial with the jth power of the first moment,
in each term of the polynomial with the jth power of the first moment, 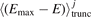 . This discrepancy increases for higher powers of j and for lower values of Ud that increase the weighting of the higher-order terms. Due to the discrepancy between the approximate (equation (6)) and the rigorous (equation (7)) expression, the velocity averaged total collision cross-sections,
. This discrepancy increases for higher powers of j and for lower values of Ud that increase the weighting of the higher-order terms. Due to the discrepancy between the approximate (equation (6)) and the rigorous (equation (7)) expression, the velocity averaged total collision cross-sections, 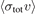 , derived from fitting the experimental data to the two expressions are systematically different. We refit the experimental data to the new expression, equation (7), for all the gas species (Xe, Ar, He, H2, N2, and CO2) reported in [1, 2]. The new values are labeled as
, derived from fitting the experimental data to the two expressions are systematically different. We refit the experimental data to the new expression, equation (7), for all the gas species (Xe, Ar, He, H2, N2, and CO2) reported in [1, 2]. The new values are labeled as 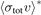 and are presented in table 1, along with the original values,
and are presented in table 1, along with the original values, 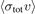 [1]. While they agree within statistical errors, the new values are systematically higher than the previous ones. As expected, the discrepancy is the largest (1.5%) for the collision partners with the lowest Ud (Rb–Xe) and least (0.4%) for Rb–He which has the largest Ud.
[1]. While they agree within statistical errors, the new values are systematically higher than the previous ones. As expected, the discrepancy is the largest (1.5%) for the collision partners with the lowest Ud (Rb–Xe) and least (0.4%) for Rb–He which has the largest Ud.
Table 1. A comparison of the experimentally determined values of 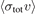 for Rb–X collisions (X = He, Ar, Xe, H2, N2, and CO2). The values of
for Rb–X collisions (X = He, Ar, Xe, H2, N2, and CO2). The values of 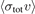 in the second column, reported in [1], are extracted by fitting the experimentally determined loss rate coefficients to the approximate expression, equation (6). The values in the column of
in the second column, reported in [1], are extracted by fitting the experimentally determined loss rate coefficients to the approximate expression, equation (6). The values in the column of  are determined by fitting the experimental data to the rigorous expression, equation (7). The discrepancy between the two values in column two and three is defined as
are determined by fitting the experimental data to the rigorous expression, equation (7). The discrepancy between the two values in column two and three is defined as 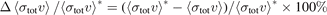 and is presented in column four. The first bracket in the columns of
and is presented in column four. The first bracket in the columns of 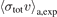 and
and 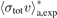 indicates the statistical error and the second one indicates the systematic error reported in [1]. The column of Ud presents the quantum diffractive energy of each collision pair, derived from the newly determined value of
indicates the statistical error and the second one indicates the systematic error reported in [1]. The column of Ud presents the quantum diffractive energy of each collision pair, derived from the newly determined value of 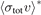 . The last column reports the updated calibration factor, ig, for the ionization gauge operated in the experiment [1], which was previously calibrated against NIST's orifice flow pressure standard only for the gas of N2. The statistical error of the calibration factor is shown in the bracket.
. The last column reports the updated calibration factor, ig, for the ionization gauge operated in the experiment [1], which was previously calibrated against NIST's orifice flow pressure standard only for the gas of N2. The statistical error of the calibration factor is shown in the bracket.
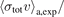 ×10−15 m3 s−1 ×10−15 m3 s−1
|
 ×10−15 m3 s−1 ×10−15 m3 s−1
|
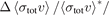 % % | Ud/kB/mK | ig | |
|---|---|---|---|---|---|
| Rb–N2 | 3.11 (5) (2) | 3.14 (5) (2) | 0.9 | 9.4 | 0.950 (19) |
| Rb–He | 2.40 (12) (8) | 2.41 (12) (8) | 0.4 | 32.3 | 0.164 (9) |
| Rb–Ar | 2.77 (5) (2) | 2.79 (5) (2) | 0.7 | 8.8 | 1.245 (26) |
| Rb–Xe | 2.71 (3) (3) | 2.75 (3) (3) | 1.5 | 5.0 | 2.549 (30) |
| Rb–H2 | 5.09 (14) (6) | 5.12 (14) (6) | 0.6 | 21.5 | 0.562 (18) |
| Rb–CO2 | 2.82 (6) (2) | 2.84 (6) (2) | 0.7 | 8.3 | 0.985 (15) |
In addition to updating the values of 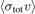 , we also report the revised gas calibration factors for the ionization gauge, ig, used in the pressure calibration experiment. The gauge was calibrated only for N2 gas by NIST (National Institute of Standards and Technology) using an orifice flow pressure standard. Our updated calibration factor, ig = 0.950 (19) agrees with the value reported by NIST, ig = 0.940 (26) [1], within 1%.
, we also report the revised gas calibration factors for the ionization gauge, ig, used in the pressure calibration experiment. The gauge was calibrated only for N2 gas by NIST (National Institute of Standards and Technology) using an orifice flow pressure standard. Our updated calibration factor, ig = 0.950 (19) agrees with the value reported by NIST, ig = 0.940 (26) [1], within 1%.
3. Conclusion
In this work, we have examined the effect of the trapped atom ensemble energy distribution on the loss rate coefficient determinations and have provided an approximate (equation (6)) and a more rigorous expression (equation (7)). We have found that the discrepancy between two expressions can lead to a systematic shift in determining the values of 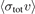 from the experimental data. Thus, we report improved
from the experimental data. Thus, we report improved 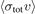 values determined by refitting experimentally measured loss rate coefficients in [1] to the new rigorous expression, equation (7). The newly determined values are systematically higher than but all within 2% of the previously reported values. These new loss rate coefficient values will increase the precision and the accuracy of the Rb based primary quantum pressure standard.
values determined by refitting experimentally measured loss rate coefficients in [1] to the new rigorous expression, equation (7). The newly determined values are systematically higher than but all within 2% of the previously reported values. These new loss rate coefficient values will increase the precision and the accuracy of the Rb based primary quantum pressure standard.
Finally, the re-evaluation of the loss rate coefficients also produced updated calibration factors for the ionization gauge calibrated by the cold atom pressure standard (see table 1). This gauge was calibrated for N2 gas by NIST using an orifice flow pressure standard. Our updated calibration factor, ig = 0.950 (19) agrees with the value reported by NIST, ig = 0.940 (26) [1], within 1%.
Acknowledgments
We acknowledge financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC/CRSNG) and the Canadian Foundation for Innovation (CFI). This work was done at the Center for Research on Ultra-Cold Systems (CRUCS). PS acknowledges support from the DFG within the GRK 2079/1 program.

