Abstract
We show that multiple Weyl and double-Weyl points (DWPs) arise in a chiral elastic system through stacking two-dimensional honeycomb mechanical structures. On the distinct kz plane, the band structures calculated from a tight-binding (TB) model exhibit Weyl points (WPs) at Brillouin vertices and DWPs at Brillouin centres. Based on the TB model, a practical chiral mechanical structure can be constructed by 3D printing technology. The numerical calculation illustrates several Weyl and DWPs as expected in our analysis of the TB model. To verify the topological feature, the topological charge of degeneracy is calculated. Within these WPs, we theoretically prove the existence of topologically protected surface modes, and their robustness against defects is also demonstrated.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
In the past decade, Weyl semimetals, which are categorised into solid state crystals and its Fermi energy is located precisely at Weyl points (WPs), have been widely researched in condensed matter physics. WPs are characterised by a nodal degeneracy with linear dispersive cones given by the Weyl Hamiltonian 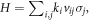 where ki, vi, and σi are wavevectors, velocities, and Pauli matrices, respectively. Intriguingly, instead of opening a gap for the degeneracy, the spatial symmetry breaking merely leads to a shift of WPs in momentum space. This robustness against geometric perturbation arises since all elements in the Weyl Hamiltonian are used. Furthermore, to determine whether a band crossing is a WP, it is necessary to calculate Berry curvatures and topological orders in the vicinity of the degeneracy. By imitating the concept of the electric field radiated from a charge, Berry curvatures can be regarded as a field emitted by a WP with certain 'topological charge' (TC) [1]. Since every WP possesses nonzero TCs, the distribution of Berry curvature exhibits the features around WPs, either a source or a sink; hence, the volume integration enclosed the corresponding WPs gives rise to the magnitude of TCs.
where ki, vi, and σi are wavevectors, velocities, and Pauli matrices, respectively. Intriguingly, instead of opening a gap for the degeneracy, the spatial symmetry breaking merely leads to a shift of WPs in momentum space. This robustness against geometric perturbation arises since all elements in the Weyl Hamiltonian are used. Furthermore, to determine whether a band crossing is a WP, it is necessary to calculate Berry curvatures and topological orders in the vicinity of the degeneracy. By imitating the concept of the electric field radiated from a charge, Berry curvatures can be regarded as a field emitted by a WP with certain 'topological charge' (TC) [1]. Since every WP possesses nonzero TCs, the distribution of Berry curvature exhibits the features around WPs, either a source or a sink; hence, the volume integration enclosed the corresponding WPs gives rise to the magnitude of TCs.
In addition to the substantial amount of theoretical and numerical predictions for the Weyl semimetals [2–10], the existence of Weyl quasiparticles has been observed in electronic [11–15] and bosonic regimes [16–20]. Besides, topological semimetals named 'type-II Weyl semimetals' have set themselves apart from the usual (type-I) Weyl semimetals. Due to the violation of Lorentz symmetry, a type-II Weyl semimetal possesses several tilt Weyl cones which makes the Fermi energy level intersect both the WPs and bulk bands [21, 22]. Compared to Type-I WPs, it causes a particular density of states. Experimental observations of type-II Weyl fermions have been discovered in a layered transition-metal dichalcogenides [23–25] and a single crystalline compound [26, 27]. For WPs, in addition to the linearly degenerate signature in all three dimensions, there are topological surface modes due to non-vanishing TCs. While topological surface modes connecting WPs were firstly measured in electronic systems [12, 13], similar phenomena have been explored extensively in acoustic [19], photonic [20], and plasmonic [28] systems.
Aside from the WPs, double-Weyl points (DWPs), which possess higher topological orders, and emerge in particular crystals with specific symmetries, have been observed in the literature [29, 30]. Unlike single Weyl points (SWPs), DWP carries TCs whose values are equal to ±2 because DWPs are the coalescence of two SWPs. In the case of DWPs, the band crossing at the degeneracy in at least one momentum plane can be expressed as the form of a quadratic dispersion. Here, the term 'quadratic dispersion' means that quadratic terms dominate the low-energy Hamiltonian. The observation of DWPs has been proposed in the crystalline solid of SiSr2 [29] and photonic crystals [6, 17].
Although a great number of research related to WPs and non-trivial surface modes have been proposed, much less study has been devoted to the elastic counterpart owing to the complexities of elastic solids. Yet, amongst all the available systems, the flexural wave in thin elastic plates is superior to other physical platforms due to several advantages. Firstly, it is feasible for a sophisticated elastic structure attributed to 3D printing technology [19, 31]. Secondly, flexural vibrating modes are strictly confined within the elastic structure, leading to relatively low radiation loss. Lastly, within the frequency region 1–100 kHz whose corresponding structure scale is up to 100 millimetres, the material loss is almost negligible for most elastic solids, making the experimental results fairly match the theoretical prediction. In this article a tight-binding (TB) model has been analysed to pave the way for the research in a real elastic system. With the aid of this TB model, we investigated the generation of multiple SWPs and DWPs in an elastic structure consisting of honeycomb chiral lattices. As the DWPs are guaranteed by some particular symmetries, breaking those symmetries splits a DWP into two SWPs. Also, the calculation of Chern number and the exhibition of topologically non-trivial surface states further validate the emergence of WPs and DWPs. As its structure is feasible with the 3D printer technology to date, the experimental realisation is expected in the near future.
TB model
The TB model for an AA-stacked honeycomb lattice is introduced. The practical elastic chiral structure will be discussed in the next section. The displacements between two nearest neighbours (NN) in the same layer is a and the lattice constant along the z direction is c. The translation vectors can be expressed as 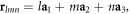 where the primitive lattice constants
where the primitive lattice constants 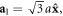
 and
and 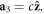 Besides, three longitudinal and transverse unit vectors connecting between the NNs are given by
Besides, three longitudinal and transverse unit vectors connecting between the NNs are given by
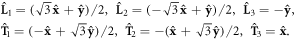
Consisting of the two p-orbital components px and py, the NN TB Hamiltonian is given by 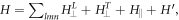 where
where
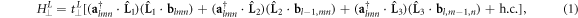
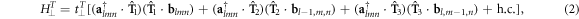
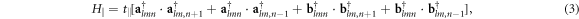
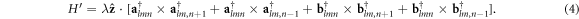
where 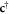 (c), c = a, b represent the creation (annihilation) vector operator and
(c), c = a, b represent the creation (annihilation) vector operator and ![${\bf{a}}({\bf{b}})={[{a}_{x}({b}_{x}),{a}_{y}({b}_{y})]}^{T}.$](https://content.cld.iop.org/journals/1367-2630/20/8/083031/revision2/njpaada55ieqn8.gif)
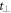 and
and 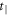 are the hopping parameters for the intralayer and interlayer. λ stands for the extra interlayer interaction resulted from the presence of cross-coupling for px and py. Being transformed to the momentum space, the Hamiltonian in terms of wavevectors k can be described by the following equation:
are the hopping parameters for the intralayer and interlayer. λ stands for the extra interlayer interaction resulted from the presence of cross-coupling for px and py. Being transformed to the momentum space, the Hamiltonian in terms of wavevectors k can be described by the following equation:
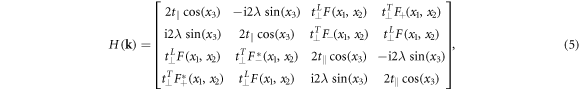
where 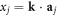 and the complex elements F and
and the complex elements F and 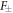 are defined by
are defined by 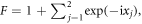
![${F}_{\pm }=1+\displaystyle {\sum }_{j=1}^{2}\exp [-{\rm{i}}({x}_{j}\pm 2\pi j/3)].$](https://content.cld.iop.org/journals/1367-2630/20/8/083031/revision2/njpaada55ieqn14.gif) With equation (5), SWPs and DWPs can be discussed through the analysis of the aforementioned TB model. From figures 1(a) to (c), the band structures along the distinct reduced Brillouin boundaries are determined in accordance with the hopping parameters
With equation (5), SWPs and DWPs can be discussed through the analysis of the aforementioned TB model. From figures 1(a) to (c), the band structures along the distinct reduced Brillouin boundaries are determined in accordance with the hopping parameters 
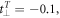
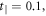 and
and 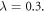 Evidently, while kz = 0 and π/c, there are two quadratic degeneracies at Γ point between 1st–2nd and 3rd–4th bands, and one linear degeneracy at K point between 2nd and 3rd bands. It is interesting to point out that for kz ≠ 0 or ±π/c, this fixed wave vector in the z direction generates effective synthetic gauge fields [5], which make the system behave as a topological Chern insulator in kx–ky sub-reciprocal plane.
Evidently, while kz = 0 and π/c, there are two quadratic degeneracies at Γ point between 1st–2nd and 3rd–4th bands, and one linear degeneracy at K point between 2nd and 3rd bands. It is interesting to point out that for kz ≠ 0 or ±π/c, this fixed wave vector in the z direction generates effective synthetic gauge fields [5], which make the system behave as a topological Chern insulator in kx–ky sub-reciprocal plane.
To clarify the topological characteristics of all the band crossings in this TB model, the Berry curvature distribution around each degeneracy needs to be checked. In classical electromagnetism, Gauss' law bridges the electric field distribution and charge magnitude. In the same manner, the Berry curvature distributions of certain degeneracies behave as a field emitted from a source or sink with a non-vanishing TC. The magnitude of TC can be obtained by taking the closed surface integral enclosed each degenerate point. From the figures 1(a) to (c), the values of TCs labelled in different colours display WP(DWP)s with ±1(2) charges at high-symmetry points K(Γ) and H(A). Whilst the boundary is cut, Fermi arc connecting a positive TC and a negative one emerges in equi-frequency contour. Figure 1(d) illustrates Fermi arcs around SWPs while several bulk regions exist due to the frequency difference between two WPs.
Figure 1. (a) The band structure based on equation (5). One SWP and two DWPs with distinct topological charges are labelled in colour. The inset illustrates the reciprocal hexagonal lattice of the TB model. Band structures along the (b) HKH and (c) AΓA boundary. Especially, at Γ and A point, the line shapes of dispersions are quadratic in kx–ky reciprocal plane but remain linear as kz changes. (d) Equi-frequency contour at zero frequency. The yellow areas are bulk regions and the red dots mark the location of SWPs. Within WPs, Fermi arcs are clearly seen.
Download figure:
Standard image High-resolution imageIt is worth noting that this TB approach is valid for modelling a p-band Hamiltonian of all periodic resonator-tunnel systems since most of the p-orbital energy is localised in the resonators except the one transferred through tunnels. The zero energy represents the natural frequency of each resonator. For example, for the flexural wave systems the natural frequency of an elastic thin disc  where D is the flexural rigidity, ρ is the density, h is the thickness of the plate, and the magnitudes of λm depend on the size and shape of resonators. Employed for the energy transfer between resonators, the bridging tunnels are related to the hopping parameters given by equations (1)–(4). If the cross-section area of tunnels is tuned qualitatively, the hopping parameter varies since the amount of energy transfer changes. These facts enable us to design the geometry by means of the results derived from TB models. However, a quantitative analysis between hopping parameters and coupling channel requires further study.
where D is the flexural rigidity, ρ is the density, h is the thickness of the plate, and the magnitudes of λm depend on the size and shape of resonators. Employed for the energy transfer between resonators, the bridging tunnels are related to the hopping parameters given by equations (1)–(4). If the cross-section area of tunnels is tuned qualitatively, the hopping parameter varies since the amount of energy transfer changes. These facts enable us to design the geometry by means of the results derived from TB models. However, a quantitative analysis between hopping parameters and coupling channel requires further study.
Elastic chiral lattice
The previous TB model discussion has offered an insight into the design of a real structure. According to the parameters given in4 , figure 2(a) illustrates an elastic chiral structure with a honeycomb lattice. The structure is made of commercial 3D printed polymers (VeroBlue RGD840) whose material parameters are ρ = 1190 kg m−3, E = 2.72 GPa, ν = 0.38 [19]. The sample preparation and a possible experimental implementation will be discussed later. The chiral tunnels in the transverse (x–y) plane eliminate all relevant types of rotational and mirror symmetries except C6 symmetry. Thus, the isolated degeneracies are guaranteed. Along the z direction, inspired by the twisted sound waveguides in [5], the designated elastic beams link to two layers. This gives rise to the flexural px–py mode coupling so that it contributes the cross terms as the one given in equation (4). Consequently, the emergence of WPs, DWPs, and topologically non-trivial elastic surface modes in terms of distinct wave vector kz are intuitively expected. Figure 2(b) depicts the two degenerate eigenmodes at K point, where the flexural fields show the characteristic of a p-orbital pattern.
Figure 2. (a) The unit cell of the elastic chiral lattice consisting of polymers. The in-plane chirality annihilates all the mirror or rotational symmetries except the C6 symmetry, and the out-of-plane one is in charge of interlayered LT coupling. The geometry parameters are denoted in footnote 4. (b) The flexural px–py eigenmodes between 1st and 2nd bands at Γ point, where red and blue parts, respectively, illustrate the positive and negative flexural waves. The band structures from (c) to (e) show similar signatures compared with figure 1. Colour circles highlight the positions and magnitudes of WPs in band structures.
Download figure:
Standard image High-resolution imageIn figures 2(c)–(e), we numerically calculate the corresponding band structure by the commercial software COMSOL v5.3. These band structures illustrate similar characteristics compared to the px–py TB model as depicted in figure 1. This fact validates that the previous analysis applies to this elastic chiral system. In figures 2(c) and (d), band structures are depicted, and they present linear dispersions in all momentum directions near the K point at 7 kHz. As a result, this phenomenon implies that these degeneracies are the candidates of SWPs. Note that the frequencies of three labelled SWPs in figure 2(d) are allowed to be different as shown in figure 1(b). In other words, the frequencies in figure 2(d) are accidentally identical; however, their frequency difference arises while the structure geometry changes. Furthermore, as shown in figure 2(c), there are two DWPs intersected by 1st–2nd and 3rd–4th bands at the centre of the Brillouin zone. And the main feature of DWPs, whose dispersions are quadratic in the transverse k plane but linear along kz direction, is also illustrated in figures 2(c) and (e).
To ensure the existence of non-vanishing TCs near the degenerate points, we numerically calculate a closed surface integration of Berry curvature enclosing these degeneracies [1, 6]. The colour circles in figures 2(c)–(e) label the TC of different WPs with ±1 and ±2 at Brillouin zone vertices and its centre. All the results are consistent with the ones given by the TB method. In figure 2(d), due to the chiral tunnels, breaking all the mirror symmetries leads to the SWPs with identical charges on the same kz plane. Moreover, since the sum of all WPs within the BZ requires neutralisation, opposite TC of SWPs in two distinct kz planes are certain such that kz = 0, ±π/c in figure 2(d).
In addition to the direct calculation of TCs, the TC of a WP can be analytically obtained by the low-energy expression by means of symmetry arguments [8, 17]. It is known that C3 symmetry generates Dirac points possessing TC of ±1 at Brillouin vertices K and K'. Henceforth, we can set the discussion of this linear degeneracy aside and zooms in on the emergence of deterministic DWPs. As for C3 rotational and time-reversal invariances in the system, in the following discussion we theoretically present that they guarantee topologically non-trivial DWPs at certain points [17] with both symmetries. Around these symmetry-invariant points, such as Γ and A, the low-energy 2 × 2 Hamiltonian can be expressed as 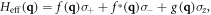 where q represents in-plane small-quantity momentum expansions from the symmetry-invariant points,
where q represents in-plane small-quantity momentum expansions from the symmetry-invariant points,  are circular superpositions of Pauli x and y components, and
are circular superpositions of Pauli x and y components, and 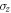 are Pauli matrix z components. As the bases of the above effective Hamiltonian are (1, 0)T and (0, 1)T, the matrix of C3 symmetry operators, denoted as
are Pauli matrix z components. As the bases of the above effective Hamiltonian are (1, 0)T and (0, 1)T, the matrix of C3 symmetry operators, denoted as 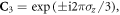 is represented. Since the effective Hamiltonian is invariant under C3 rotation, one obtains
is represented. Since the effective Hamiltonian is invariant under C3 rotation, one obtains
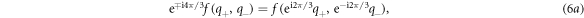
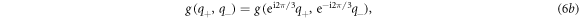
where 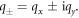 As the time-reversal invariance leads to the relation that
As the time-reversal invariance leads to the relation that 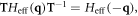 coefficient function f must be an even function under the time-reversal invariant condition. If f can be expanded as
coefficient function f must be an even function under the time-reversal invariant condition. If f can be expanded as 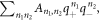 combining the above arguments ensures all linear terms vanish. It makes the lowest expansions become quadratic, and then TCs of ±2 arise. Besides, if time-reversal symmetry is broken, DWPs still survive as long as the C6 symmetry in the system is preserved [8].
combining the above arguments ensures all linear terms vanish. It makes the lowest expansions become quadratic, and then TCs of ±2 arise. Besides, if time-reversal symmetry is broken, DWPs still survive as long as the C6 symmetry in the system is preserved [8].
When added perturbations break the symmetry, one of the effects for WPs is that the perturbation only moves the position of WPs in momentum space rather than lift a gap. As a result, if one breaks the symmetry which guarantees the deterministic DWP, DWP will split into two SWPs in the momentum space but make no gaps emerge. In figure 3(a), the C3 symmetry in the elastic chiral lattice is broken by filling two tungsten carbide plates (ρ = 15 520 kg m−3, E = 600 GPa, ν = 0.2) with opposite isosceles triangular shapes into AB sublattice. The side and the bottom of the triangles are R/2 and R/3 in length, respectively. In the kz = 0 plane, figures 3(b), (c) illustrate 3D band structures exhibiting two SWPs evolving from DWP. Two SWPs are located at the coordinates (kx, ky, f) = (∓0.05π/a, ∓0.05π/a, 5.06 kHz) between 1st and 2nd bands, and (kx, ky, f ) = (±0.02π/a, ∓0.08π/a, 8.20 kHz) between 3rd and 4th bands. The coordinates of SWPs on the same plane are opposite to each other owing to the presence of C2 rotation in the z axis. As both SWPs are separated from a DWP, they have the identical charge magnitudes because of the conservation of TCs. The above discussion shows the robustness of WPs against the symmetry violation as the shift occurs in the k space and no gap is opened.
Figure 3. (a) Two oppositely directional isosceles triangles are embedded in the chiral lattice to break C3 symmetry. After eliminating C3 symmetry, two SWPs split from the DWP between (b) 1st–2nd and (c) 3rd–4th bands arise.
Download figure:
Standard image High-resolution imageRobust surface modes
The emergence of topological boundary modes may be one of the most essential properties in topological materials. With a fixed kz value, the off-diagonal terms resulting from the chiral interlayer coupling in equation (5) can be considered a synthetic gauge field in a 2D subsystem [5, 6], and it lifts non-trivial bandgaps where topologically protected boundary modes arise. Figure 4(a) presents the band structure with fixed kz = π/2c. Due to the presence of the band Chern numbers marked in figure 4(a), there are two topologically non-trivial bandgaps guaranteed by bulk-boundary correspondence. In figure 4(b), we illustrate the projected band structures on the kz = π/2c plane, which shows topological surface modes obtained by numerically calculating a 1 × 15 super-cell elastic chiral lattice with truncation along x axis. The surface modes coloured in red and green represent the upper and lower boundaries, respectively. At kz = π/2c and f = 6.70 kHz, the elastic waves travel along the truncated surface in one direction and propagate robustly against the defect, as shown in figure 4(c). Besides, while kz = −π/2c, the elastic wave in figure 4(b) propagates along the counter-clockwise direction due to the presence of negative group velocity. Yet, the elastic wave is still under topological protection as it passes through a sharp corner without reflections.
Figure 4. (a) Fixing kz values as the synthetic gauge field for the band structure in the 2D subdomain. Numbers attached to bands denote the corresponding Chern numbers. (b) Projected band structure with truncation along x axis. Topological surface modes are coloured in red and green to differ from the surface modes located at the upper and lower boundaries. On the different kz planes, the surface modes with topological protection are demonstrated in (c) and (d).
Download figure:
Standard image High-resolution imagePossible experimental implementation
In this section the possible experimental implementation is discussed. To implement the proposed elastic chiral lattice, a commercial 3D printer named Stratasys Objet30 Pro may be employed as its accuracy can be controlled to 0.1 mm [32]. In addition, due to the weight of the structure, severe deformation or brokenness of the elastic lattice on the bottom beams or layers should be taken into account. To avoid potential damage to samples, the height H between layers or the diameters D of interlayer beams can be raised to provide better mechanical supports. Since the symmetries are unchanged, these modifications of geometry will not eliminate WP and the physics discussed earlier still apply. For the WP measurement, with the aid of a commercial tool, named PSV-400 laser scanning vibrometer, the data of vibrating modes can be acquired [32]. To obtain WPs and their Fermi arcs, one can collect data at every spatial point and then convert them into momentum space via Fourier transform. A similar approach for electromagnetic WPs and Fermi arcs measurement can be found in [20].
Conclusion
In conclusion, multiple SWPs and DWPs in an elastic chiral lattice have been proposed. The works start from a TB model whose band structure exhibits SWPs at Brillouin vertices and DWP at Brillouin centres. The magnitudes of TCs have been verified so that the topological characteristics for WPs are ascertained. Between these TCs, Fermi arcs emerge as they have been demonstrated in an equi-frequency contour. To verify the validity of this TB model, we have demonstrated an elastic structure by periodically connecting honeycomb lattices with chiral bridges. The appearances of both band structures are similar while the proper parameters in the TB model are designated. At kz = 0 or ±π/a, SWPs and DWPs arise in the same position as the TB model has provided. Furthermore, we have demonstrated the topological boundary modes in the system while kz = ±π/2c. Both cases exhibit topological protection since no backscattering is generated when the waves hit a defect. Finally, possible implementations for sample preparation and data acquirement have been discussed.
Footnotes
- 4
The geometry parameters are shown as follows: a = 30, R = 7.5, t = 3, L = 2(a2/4 − R2)1/2, H = 2, d = 4, D = 2, and l = 5. All parameters are in the unit of millimetre.







