Abstract
Stainless steels are susceptible to localized forms of corrosion attack, such as pitting. The size and lifetime of a nucleated pit can vary, depending on a critical potential or current density criterion, which determines if the pit repassivates or continues growing. This work uses finite element method (FEM) modeling to compare the critical pit radii predicted by thermodynamic and kinetic repassivation criteria. Experimental electrochemical boundary conditions are used to capture the active pit kinetics. Geometric and environmental parameters, such as the pit shape and size (analogous to additively manufactured lack-of-fusion pores), solution concentration, and water layer thickness were considered to assess their impact on the pit repassivation criterion. The critical pit radius (the transition point from stable growth to repassivation) predicted for a hemispherical pit was larger when using the repassivation potential (Erp) criteria, as opposed to the current density criteria (pit stability product). Including both the pit stability product and Erp into its calculations, the analytical maximum pit model predicted a critical radius two times more conservative than the FEA approach, under the conditions studied herein. The complex pits representing lack-of-fusion pores were shown to have minimal impact on the critical radius in atmospheric conditions.
Export citation and abstract BibTeX RIS
List of symbols
| D | Cathode diameter |
| Ebase | FEM-calculated electrolyte potential at pit base |
| Eedge | FEM-calculated electrolyte potential at cathode edge |
| Emouth | FEM-calculated electrolyte potential at pit mouth |

| Open circuit potential of cathode |
| Erp | Repassivation potential |
| f | Degree of critical pit solution saturation required to maintain stable propagation |
| I LC | Anodic current demand |
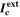
| Ideal cathodic current capacity |
| I crit | Critical current which satisfies the pit stability product in a given scenario |
| I FEM | FEM-calculated current |
| ( i · x )crit | 1-D pit stability product at critical salt film saturation (50% used in this work) |
| ( i · x )sf | 1-D pit stability product at 100% salt film saturation |

| 3-D hemispherical pit stability product at critical salt film saturation (50% used in this work) |
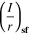
| 3-D hemispherical pit stability product at 100% salt film saturation |
| LD | Loading density |
| PDS | Potentiodynamic scan |
| r | Pit mouth radius |
| r crit | Critical pit radius when a stability criterion is satisfied |
| RH | Relative humidity |
| rmax | The maximum pit radius derived from the maximum pit model |
| WL | Water layer thickness |
| x | 1-D pit depth |
Metals with a passive film, such as stainless steel (SS) and aluminum, are susceptible to the localized corrosion phenomenon of pitting. 1 It is commonly agreed in literature that there are three main stages in pitting; (1) nucleation, which includes the local breakdown of a passive film; (2) metastable pitting, in which a nucleated pit repassivates; and (3) stable growth, in which pits spontaneously continue growing. 1–4 Recognizing under which conditions the transition from (2) metastable to (3) stable pitting will occur is extremely important, as pits can be difficult to detect or mitigate once initiated. 5 Left unmitigated, pits can grow to hundreds of microns in size, 6,7 leading to the potential for component failure by perforation or environmentally assisted cracking with the pit acting as the stress concentrator. 8–10
For additively manufactured (AM) passive metals, processing defects including lack-of-fusion (LoF) porosity have been shown to act as preferential initiation sites for pitting. The studies to date investigating porosity's influence on pit initiation have been carried out with experimental methods utilizing polarization measurements under full immersion environments. These experiments provide information on a pore's propensity to initiate a pit, but lack the dexterity to assess how a pit, once initiated in the pore, can maintain the required chemistry to propagate pit growth at open circuit conditions (a more likely real-world scenario). If a pit initiates inside a pore, then aspects of the pore's geometry such as aspect ratio, tortuosity, etc, may control diffusion of ions in and out of the pore, determining if that pit remains active or repassivates. Furthermore, a recent perspective has shown that in materials prone to pitting (such as the porous AM surface described above), the rate limiting step is not the initiation of pits but rather the transition from metastable to stable growth.
2
The current study develops a steady-state finite element method (FEM) model, which assumes a metastable pit has initiated inside a computer generated surface pore and focuses on using electrochemical criteria to predict a critical radius defining a threshold of when the pit will transition to stable growth or repassivate (growth stops). The model is then broadly applied to metastable pits under different pore geometries and environmental parameters. Determining a criterion to predict whether or not an initiated pit will continue growing or will repassivate has been heavily researched. Pitting criteria based on exceeding a critical potential, such as the pitting potential (Epit) and the repassivation potential (Erp), are thresholds that can be identified empirically using potentiodynamic scans (PDS). Traditionally, Epit has been thought to represent a threshold at which pits are able to stably grow and is commonly determined by a sharp increase in current density to a stable value defined by the mass transport limitations of the corroding system during an anodic PDS.
11,12
Below Erp
 which has also been referred to as the protection potential, lies a threshold at which all pits stop nucleating and growing.
3,11,13,14
Erp is generally considered the lower bound for pitting, making it a popular parameter when discussing a conservative approach to pit prediction.
13,15
which has also been referred to as the protection potential, lies a threshold at which all pits stop nucleating and growing.
3,11,13,14
Erp is generally considered the lower bound for pitting, making it a popular parameter when discussing a conservative approach to pit prediction.
13,15
Rather than using a voltage criterion, the mass transport characteristics of maintaining a stable pit can be used to determine a kinetic-based criteria. Galvele proposed that a certain pit stability product (i·x) was needed to maintain the pit chemistry at the base of a 1-D pit in order to allow continued growth, in which the rate of dissolution (i) at the base of the pit with depth (x) is in competition with diffusion out of the pit. It was demonstrated that the product (i·x) could be used to determine the chemical composition at the bottom of the pit. Vetter & Strehblow, among other researchers, extended the 1-D (i·x) to a 3-D criterion  which is more applicable to the higher spatial dimensionality of pits in bulk samples.
4,16–19
In the 3-D criterion I is the current and
which is more applicable to the higher spatial dimensionality of pits in bulk samples.
4,16–19
In the 3-D criterion I is the current and  is the hemispherical pit radius. Straightforward measurements of 1-D pit electrodes (i.e., using artificial pits or lead-in-pencil electrodes), in which the limiting current density ilim is extracted at a variety of pit depths, allows determination of (i·x) for salt film (sf) conditions (i.e., 100% saturation of the solution with respect to metal chlorides at the bottom of the pit), (i·x)sf and, thus,
is the hemispherical pit radius. Straightforward measurements of 1-D pit electrodes (i.e., using artificial pits or lead-in-pencil electrodes), in which the limiting current density ilim is extracted at a variety of pit depths, allows determination of (i·x) for salt film (sf) conditions (i.e., 100% saturation of the solution with respect to metal chlorides at the bottom of the pit), (i·x)sf and, thus,  .
5,20–23
However, the presence of a salt film at the bottom of the pit is not necessary for pit growth, as shown by observation of crystallographic facets within pits,
24
making the above criteria too conservative. Using artificial SS304 pits, Gaudet was the first to conclude that pitting occurred when the concentration at the pit surface was between 60% and 80% saturation.
25
More recent work has suggested that the critical saturation concentration may actually be as low as 43%–50% of the fully saturated concentration.
22,26
.
5,20–23
However, the presence of a salt film at the bottom of the pit is not necessary for pit growth, as shown by observation of crystallographic facets within pits,
24
making the above criteria too conservative. Using artificial SS304 pits, Gaudet was the first to conclude that pitting occurred when the concentration at the pit surface was between 60% and 80% saturation.
25
More recent work has suggested that the critical saturation concentration may actually be as low as 43%–50% of the fully saturated concentration.
22,26
Chen & Kelly developed a mathematical model incorporating multiple pit threshold criteria to determine the maximum radius (rmax) that a hemispherical pit can attain under thin electrolytes for atmospheric environments.
27
The concept is based on combining Erp, (i·x)crit, ohmic drop in thin electrolytes, and the finite kinetics of cathodic reactions. The potential threshold, Erp, creates a bound above which the pit mouth must remain for stability, as observed experimentally. The ohmic drop, combined with the finite cathodic kinetics, defines the maximum cathodic current 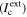 available to support pit growth. The calculation of
available to support pit growth. The calculation of  takes advantage of the fact that only the total cathodic current supplied to the pit is needed; the actual spatial distribution of the current is not important in determining pit stability. Thus, a mathematically equivalent cathode was constructed for which
takes advantage of the fact that only the total cathodic current supplied to the pit is needed; the actual spatial distribution of the current is not important in determining pit stability. Thus, a mathematically equivalent cathode was constructed for which  is constant with position and is quantitatively equal to that of the maximum possible current that the actual cathode could provide given its electrochemical kinetics and the solution conductivity and thickness of the water layer. The finite ideal cathode size to maintain stable pit propagation can be back-calculated based on the given conditions.
27
If conditions are such that more anodic current (ILC) is required than
is constant with position and is quantitatively equal to that of the maximum possible current that the actual cathode could provide given its electrochemical kinetics and the solution conductivity and thickness of the water layer. The finite ideal cathode size to maintain stable pit propagation can be back-calculated based on the given conditions.
27
If conditions are such that more anodic current (ILC) is required than  the pit will stifle due to dilution of the aggressive pit environment. Stable pitting only occurs when ILC is equal to or less than
the pit will stifle due to dilution of the aggressive pit environment. Stable pitting only occurs when ILC is equal to or less than  27
Both currents, ILC and
27
Both currents, ILC and 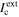 depend on r, so ILC =
depend on r, so ILC =  defines the magnitude of rmax. The effects of environmental variables on the mathematical model's prediction of rmax have been studied, from water layer thickness (WL) and relative humidity (RH) effects to solution chemistry considerations.
19,23,28
Although the maximum pit model predicts the maximum radius that a 3-D hemispherical pit may grow under a given set of conditions, the question remains as to the level of conservatism it represents when compared to a non-ideal system. Furthermore, the maximum pit model predicts stability through a combination of Erp and (i·x)crit; separately, the predicted results from these pit stability criteria have never been compared.
defines the magnitude of rmax. The effects of environmental variables on the mathematical model's prediction of rmax have been studied, from water layer thickness (WL) and relative humidity (RH) effects to solution chemistry considerations.
19,23,28
Although the maximum pit model predicts the maximum radius that a 3-D hemispherical pit may grow under a given set of conditions, the question remains as to the level of conservatism it represents when compared to a non-ideal system. Furthermore, the maximum pit model predicts stability through a combination of Erp and (i·x)crit; separately, the predicted results from these pit stability criteria have never been compared.
Most modeling of stainless steel pits has focused on either 1-D
3,22,29–31
or hemispherical
29,32,33
geometries, due to their mathematical simplicity, with a few recent works using a deformable mesh to investigate the evolution of more complex geometries.
34–36
The work performed here focuses on predicting the stability of four computer-generated pit geometries that represent two common observations from corrosion experiments (1-D and hemispherical pits) as well as two complex-shaped pits, similar to LoF pores found in AM metals. A steady-state FEM model was built to explore how potential and current distributions vary across four stainless steel (SS316) pit geometries, as a function of r, x, WL, and cathode diameter (D). Then, two pit stability criteria were employed; Erp and (i·x) for 1-D pits and Erp and  for 3-D pits, to determine if the pits will remain growing or repassivate. Results calculated using more realistic cathodic boundary conditions in comparison to assuming an ideal cathode were also discussed.
for 3-D pits, to determine if the pits will remain growing or repassivate. Results calculated using more realistic cathodic boundary conditions in comparison to assuming an ideal cathode were also discussed.
Computational Procedure/Process
Computational governing equation
The FEM model was conducted using the Corrosion Module in COMSOL Multiphysics© (version 5.5). In all calculations, the migration of Cl− ions was assumed to transport all of the current, due to the high concentration of supporting NaCl electrolyte in both 3 M and 0.6 M NaCl scenarios considered. The main mass transport mechanism within a pit is conventionally assumed to be diffusion, thus following Fick's laws. However, recent work has shown that migration within the pit is not negligible, 31 and may even contribute up to two thirds of the limiting current density. 37 Therefore, this work will assume that migration is dominant over diffusion or convection, thereby allowing for the full Nernst-Planck equation to be simplified into,
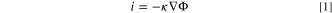
where i is the current density, κ is the conductivity, and Φ is the potential in the electrolyte. Accounting for the conservation of charge ( i = 0), the Laplace (Eq.2) can be derived and used to solve for the potential.
i = 0), the Laplace (Eq.2) can be derived and used to solve for the potential.

The potential on the electrode surface (E) was calculated by taking the inverse sign of the electrolyte potential, at the electrode/electrolyte interface (Eq. 3).
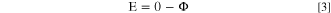
A thorough discussion of utilizing the Laplace equation, in lieu of the full Nernst-Plank equation, is described in a recent review paper by Liu & Kelly. 38 In line with the Laplace equation, the water layer domain was assumed to have a constant bulk conductivity (κbulk), that is, assuming that the solution is homogeneous and well-mixed. Values of conductivity were calculated via OLI Studio Analyzer© 9.5 (OLI Systems, Inc., Cedar Knolls, NJ) software to be 19.7 S m−1 for 3 M NaCl and 5.5 S m−1 for 0.6 M NaCl.
Simulated pit geometries
Four pit shapes were studied, two geometrically simple pits and two more geometrically complex pits. To reduce the computational cost, all of the geometries were built in a 2-D domain which was axisymmetric about the z -axis (Fig. 1). Note that the parameter D is on the order of cm, and therefore the entire electrolyte domain is not shown in Fig. 1 due to the extremely small aspect ratio. The two simple pits consisted of a hemispherical and rectangular pit, representing a 3-D and 1-D pit, respectively. These geometries are commonly used to represent pitting corrosion in modeling, because of their mathematical simplicity. 3,22,29,30,32,33 However, in realistic structures, pitting morphologies are not constrained to geometric simplicity. Therefore, complex pit geometries, based as an extension of the hemispherical pit, were created to represent common surface defects to both wrought and AM structures. These geometries consisted of a "double pit" and an "undercutting pit" (Figs. 1c and 1d).
Figure 1. Various pit geometries built in the model, with geometric parameters labeled as the water layer thickness (WL), pit mouth radius (r), cathode diameter (D), and depth of a rectangular pseudo-1-D pit (x); (a) and (b) simple pits; (c) and (d) complex pits. The blue surfaces represent active anodic dissolution.
Download figure:
Standard image High-resolution imageFor consistency, the opening pit radius r in all of the geometries was equal, although the total anodic surface area was not. This distinction can be seen in Fig. 1, denoted by r in comparison to the blue anodic surfaces. In order of increasing active anodic surface area, the geometries are the double pit, rectangular pit, hemispherical pit, and undercutting pit (with all regions active). A variable mesh was built on all geometries, to allow for finer resolution along the actively dissolving surfaces and the z-axis of symmetry (Fig. 2). The mesh was coarser along D to limit computational cost. Parameter sweeps of r, x, WL, and D were conducted to determine the magnitude of effect each parameter had on the pit stability.
Figure 2. The FEM model mesh construction of 2-D axisymmetric hemispherical (r = 15 μm, D = 30 cm, and WL = 16 μm) pit, with the boundary conditions labeled on each surface; the red dashed line represents the rotational axis.
Download figure:
Standard image High-resolution imageAfter each simulation, the distribution of potential in the system and the current density along the surface of the pit were calculated. The current density was integrated over the anodic surfaces in order to determine the total anodic current of the system. In all models, the total anodic current equaled the total cathodic current, with less than 0.25% difference.
In all pit geometries except the rectangular pit, a constant κbulk was assumed throughout the entire domain. Although simplifications within the Laplace equation limit the model from solving κ as a function of evolving species, a linear gradient inside the rectangular pit was invoked manually to account for a singular concentration gradient. Quasi-linear concentration gradients have been observed within a 1-D pit, so long as the pit is stable and a passive film is not present. 30 The concentration gradients were assumed to be more relevant for the 1-D, rather than 3-D, geometries due to the more constrained diffusion path. Steady-state conductivity of 3 M NaCl solution within the pit (κpit) was calculated via OLI Studio Analyzer© to be 21.8 S m−1, assuming a saturated metal salt film (∼5 M) to represent the worst-case scenario. The linear gradient was constrained to have κpit at the base of the pit and κbulk at the mouth of the pit, varying along the z-axis as a function of x. Although ∆κ was not very large (2.1 S m−1), at a constant pit depth of 10 times the pit radius, the absence of a linear gradient was seen to lower the current by 0.18 μA which was a 3% difference of the total currents.
Boundary conditions
Cathodic and anodic PDS were input into the model as boundary conditions to represent the behavior of SS316 at room temperature in two different NaCl concentrations. The PDS were input as a function of the electrode potential (Fig. 2). Although not visible, the far field boundary conditions used the same insulating conditions as imposed on the top surface of the electrolyte. The activated pit scans were conducted via lead-in-pencil experiments, to capture the behavior of an actively corroding pit, with a scan rate of 50 mV s−1 starting with the pit under salt film conditions and scanning in the negative direction. Anodic and cathodic Tafel slopes were extracted from the active pit polarization curves and were input separately into the model.
The procedure for determining the cathodic kinetics was the same as Katona et al.
23
Briefly, cathodic kinetics were determined in solutions less corrosive than NaCl in order to prevent convolution of the cathodic kinetics with anodic dissolution due to open circuit localized corrosion.
27
Sodium bromide (NaBr) was chosen as it was shown to be less corrosive than NaCl as characterized by transient free OCP values and a post-scan visual inspection of the surface revealing no pitting. Concentrations of surrogate catholyte solutions of NaBr (0.73 M and 7.34 M to represent 0.6 M and 3 M NaCl, respectively) were determined based on the Levich equation concerning the mass transfer diffusion limited current density for oxygen reduction.
39
Thus, based on the Levich equation, the concentration of NaBr which matched the quantity of ilim ∝  for NaCl solutions at a given temperature was chosen. In order to determine this quantity, the solution thermodynamics database of the OLI Studio Analyzer© software was utilized. The quantity of
for NaCl solutions at a given temperature was chosen. In order to determine this quantity, the solution thermodynamics database of the OLI Studio Analyzer© software was utilized. The quantity of  was first calculated for NaCl at the desired concentration given by experimental parameters. The solution of NaBr that matched the given quantity was then chosen as the surrogate solution. The efficacy of this has been shown by Liu et al.
40
Cathodic polarizations were scanned from OCP (after 1 h stabilization) in the negative direction at a scan rate of 0.167 mV s−1 until a final potential of −0.7 VSCE.
was first calculated for NaCl at the desired concentration given by experimental parameters. The solution of NaBr that matched the given quantity was then chosen as the surrogate solution. The efficacy of this has been shown by Liu et al.
40
Cathodic polarizations were scanned from OCP (after 1 h stabilization) in the negative direction at a scan rate of 0.167 mV s−1 until a final potential of −0.7 VSCE.
Stability thresholds considered
Three different stability criteria were assessed on the simulated pit geometries, to determine whether the pit will repassivate or grow with the given set of parametric conditions:
- 1)Emouth > Erp
- 2)

- 3)

Where Emouth is the potential at the mouth of the pit, Erp is the repassivation potential, i is the current density, x is the pit depth (in a rectangular-pit context), I is the current from the pit, and r is the pit radius (in a hemispherical-pit context). In each of the criteria, if the inequality is true, then the pit is predicted to grow. Conversely, if the inequality is false, then spontaneous repassivation is predicted to occur.
Results
Measured Pit stability criteria
Both Erp and (i·x)sf were determined through successive lead-in-pencil measurements based on the procedure of Srinivasan et al., while  was calculated from (i·x) data
5,12,25,41
(Table I). The first criterion, Erp, is well known as a critical threshold for both pitting and crevice corrosion
22
and is applicable to predict the stability of all pit geometries. Conversely, the (i·x) stability criterion assumes a 1-D pit, and has been shown to be an accurate representation of the mass transport in a 1-D pit for pit depths
was calculated from (i·x) data
5,12,25,41
(Table I). The first criterion, Erp, is well known as a critical threshold for both pitting and crevice corrosion
22
and is applicable to predict the stability of all pit geometries. Conversely, the (i·x) stability criterion assumes a 1-D pit, and has been shown to be an accurate representation of the mass transport in a 1-D pit for pit depths  eight to ten times greater than r.
11
The last criterion,
eight to ten times greater than r.
11
The last criterion,  is an extension of (i·x) making it applicable to 3-D hemispherical pit geometries.
4,16–19
is an extension of (i·x) making it applicable to 3-D hemispherical pit geometries.
4,16–19
Table I. Pit stability criteria for SS316 in 0.6 M NaCl and 3 M NaCl.
| Solution Concentration of NaCl [M] | Erp [VSCE] |
 [A m−1] [A m−1] | (i·x)sf [A m−1] |
|---|---|---|---|
| 0.6 | −0.218 | 2.7 | 0.9 |
| 3 | −0.227 | 1.5 | 0.5 |
As pitting can occur when a salt film is not present on the surface of the pit, (i·x)crit can be calculated through the degree of pit solution saturation required to maintain stable propagation, f, through (i·x)crit = f (i·x)sf. The ILC required for a pit of radius  to grow stably as a hemisphere, rather than a 1-D pit, can be calculated by,
to grow stably as a hemisphere, rather than a 1-D pit, can be calculated by,
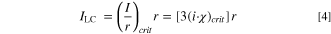
The calculation of ILC is directly related to the pit stability product for a hemisphere, as described in Chen & Kelly.
27
That is, for a 3-D hemispherical pit, the pit stability product is defined as  which can be related to (i·x) by a geometric factor of three.
4,16,17,19
Both the second and third criteria above represent the minimum current required to maintain a sufficiently low pH against dilution by diffusion.
which can be related to (i·x) by a geometric factor of three.
4,16,17,19
Both the second and third criteria above represent the minimum current required to maintain a sufficiently low pH against dilution by diffusion.
Recent findings in literature have suggested that f is between 43% to 50%;
22,26
in this work, we will assume f = 50% saturation unless otherwise noted. The measured (i·x) and calculated  values for all pit stability criteria under full salt film conditions are shown in Table I and are consistent with values seen in literature.
21–23
values for all pit stability criteria under full salt film conditions are shown in Table I and are consistent with values seen in literature.
21–23
Potentiodynamic scans
Anodic polarization scans were conducted on SS316 in 3 M and 0.6 M NaCl solution, while cathodic polarization data were generated in a NaBr solution equivalent to 3 M and 0.6 M NaCl solution in terms of diffusion-limited ORR kinetics, all at room temperature (Fig. 3). Note that all potentials in this work are in reference to a saturated calomel electrode (SCE). Both cathodic and anodic curves had little distinction between the two environments, albeit with ilim in 3 M NaCl being slightly lower (1 × 10−5 A cm−2) in comparison to ilim for ORR in 0.6 M NaCl (2 × 10−5 A cm−2), as indicated in Fig. 3. In this work, 3 M NaCl was the main solution of interest.
Figure 3. Cathodic and anodic potentiodynamic scans of SS316 in (a) 3 M NaCl and (b) 0.6 M NaCl.
Download figure:
Standard image High-resolution imageThe anodic and cathodic Tafel slopes of the lead-in-pencil anodic polarization scans were determined to be 33 mV/decade and 115 mV/decade, respectively, in 3 M NaCl. Similarly, in the 0.6 M NaCl environment, anodic and cathodic Tafel slopes were determined to be 40 mV/decade and 110 mV/decade, respectively (Fig. 3). Both anodic and cathodic Tafel slopes were imported into the model as boundary conditions on the active pit surfaces, for each respective environment, to account for localized cathodic reactions among the active pit dissolution (Fig. 2). Reversible potentials were chosen at a constant exchange current density along the Tafel slopes, representing a computational limit rather than the true electrochemical parameters Table II). The cathodic polarization scans were used as boundary conditions on the large exterior surface in the system, which represented the main source of cathodic reactions (Fig. 2).
Table II. Computational input parameters.
| Solution [M] | Parameter | Description | Value |
|---|---|---|---|
| 0.6 | βa | Anodic Tafel slope | 40 mV/decade |

| Anodic reversible potential | −0.368 VSCE | |

| Anodic exchange current density | 1.02 × 10−5 A cm−2 | |
| βc | Cathodic Tafel slope | 110 mV/decade | |

| Cathodic reversible potential | −0.036 VSCE | |

| Cathodic exchange current density | 1.02 × 10−5 A cm−2 | |
| κbulk | Bulk solution conductivity | 5.5 S m−1 | |
| 3 | βa | Anodic Tafel slope | 33 mV/decade |

| Anodic reversible potential | −0.3157 VSCE | |

| Anodic exchange current density | 6.6 × 10−7 A cm−2 | |
| βc | Cathodic Tafel slope | 115 mV/decade | |
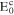
| Cathodic reversible potential | −0.1672 VSCE | |
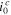
| Cathodic exchange current density | 6.6 × 10−7 A cm−2 | |
| κbulk | Bulk solution conductivity | 19.7 S m−1 | |
| κpit | Solution conductivity within a pit, assuming saturated metal salt film | 21.8 S m−1 |
Maximum pit model construction
To support dissolution of an active pit, ILC and  were calculated as a function of r, following the same procedure as Katona et al.
23
Conditions representing 50% and 100% salt film were considered and compared in the ILC calculations, although stability at 50% saturation was the main focus of this work. The intersection between the anodic and cathodic curves predicts the maximum size at which a pit can grow before repassivating as shown in Fig. 4. In 3 M NaCl, rmax of a 3-D hemispherical pit is indicated by arrows for both 50% and 100% salt film conditions. Any combination of ILC and
were calculated as a function of r, following the same procedure as Katona et al.
23
Conditions representing 50% and 100% salt film were considered and compared in the ILC calculations, although stability at 50% saturation was the main focus of this work. The intersection between the anodic and cathodic curves predicts the maximum size at which a pit can grow before repassivating as shown in Fig. 4. In 3 M NaCl, rmax of a 3-D hemispherical pit is indicated by arrows for both 50% and 100% salt film conditions. Any combination of ILC and  that falls in the region bounded by the two currents, and below rmax, predicts stable pit growth. The hatched region represents stability if 50% saturation is required, while the cross-hatched region represents stability if 100% saturation is required, showing that less saturation results in both a greater rmax and greater stable region for pit growth (Fig. 4a).
that falls in the region bounded by the two currents, and below rmax, predicts stable pit growth. The hatched region represents stability if 50% saturation is required, while the cross-hatched region represents stability if 100% saturation is required, showing that less saturation results in both a greater rmax and greater stable region for pit growth (Fig. 4a).
Figure 4. Maximum pit model calculations for an environment of (a) 3 M NaCl, with WL = 16 μm, RH = 88.3%, and LD = 3 g m−2 and (b) 0.6 M NaCl, with both the conditions of WL = 16 μm consistent with (a) and LD = 3 g m−2 consistent with (a). Note the differences in the ordinate between (a) and (b).
Download figure:
Standard image High-resolution imageTwo NaCl concentrations, 3 M and 0.6 M, were considered to represent the equilibrium solution concentration at a RH of 88.3% and 98%, respectively (Fig. 4). Changes to WL represented changes in LD while RH, κ, and by extension salt concentration were held constant, as described in Chen et al.
42
Therefore, when comparing the 3 M NaCl and 0.6 M NaCl scenarios, one can consider that either the WL or the LD between them was the same, while the remaining parameter was independent. This difference can be seen in the 0.6 M NaCl cathodic current capacity (Fig. 4b), in which the red curve represents a WL that is consistent with 3 M NaCl and the violet curve represents a LD that is consistent with 3 M NaCl. Choosing the consistent parameter can have large impacts on the maximum pit predictions, as denoted by  salt film in Fig. 4b (13 μm for LD = 0.7 g m−2 and 118 μm for LD = 3.0 g m−2). It is important to note that although
salt film in Fig. 4b (13 μm for LD = 0.7 g m−2 and 118 μm for LD = 3.0 g m−2). It is important to note that although  depends on environmental factors and cathodic kinetics, ILC only depends on geometric factors of the pit and (i·x), as seen in Eq. 4.
27
Therefore, ILC at both 100% and 50% salt film saturation does not change with WL or LD (Fig. 4b).
depends on environmental factors and cathodic kinetics, ILC only depends on geometric factors of the pit and (i·x), as seen in Eq. 4.
27
Therefore, ILC at both 100% and 50% salt film saturation does not change with WL or LD (Fig. 4b).
Simple hemispherical pit stability
The hemispherical pit was the first geometry of interest, as it represented a widely considered case in which the pit surface undergoes uniform dissolution and is a pore shape commonly seen in polished AM metals (Fig. 1a). 43,44 The parameter r was varied from 15–500 μm in a 3 M NaCl environment, while WL was held constant at 16 μm and D was held constant at 15 cm. These combinations resulted in the cathode to anode surface area ratio ranging from 1.25 × 107 to 1.12 × 104.
The electrolyte potential distribution from a single 15 μm radius pit can be seen near the vicinity of the pit (Fig. 5a) and spatially along the cathode radius to the pit mouth (Fig. 5b). To easily visualize the potential distributions over the entire parameter space tested, the potentials at three different points in the geometry were extracted as a function of r (Fig. 5c). These points were at the base of the pit (Ebase), the mouth of the pit (Emouth), and the farthest edge of the cathode from the anode (Eedge), as indicated in Fig. 5a. Note that due to the extreme aspect ratio of the geometry, the true edge of the cathode is not visible in Fig. 5a; however, the black point of Eedge is included for symbolic reasons. Physically, the potential at the edge of the cathode cannot exceed the open circuit potential of the cathode  That is, the inequality Eedge <
That is, the inequality Eedge <  must be valid at all points in the system to be physically attainable. To maintain pit stability, the potential at the mouth of the pit must be greater than the Erp, as described in the first stability criterion. Therefore,
must be valid at all points in the system to be physically attainable. To maintain pit stability, the potential at the mouth of the pit must be greater than the Erp, as described in the first stability criterion. Therefore,  and Erp were included in Fig. 5c as an upper and lower bound to maintaining stable pit growth. All potentials decreased with increased r values. From the intersection of Emouth and Erp, as indicated by a circle in Fig. 5c, radii less than 420 μm were predicted to be stable under the given set of conditions.
and Erp were included in Fig. 5c as an upper and lower bound to maintaining stable pit growth. All potentials decreased with increased r values. From the intersection of Emouth and Erp, as indicated by a circle in Fig. 5c, radii less than 420 μm were predicted to be stable under the given set of conditions.
Figure 5. 3 M NaCl hemispherical pit, WL = 16 μm, D = 15 cm; (a) 270° volumetric potential distribution at r = 15 μm; potential distribution as a function (b) spatially along the cathode to the pit mouth, and (c) of r; (d) inset of (c) showing a close-up of the potential distribution with D = 1 cm. Note the blue, red, and black spheres in (a) represent the points at which the potential was calculated in (c) and (d).
Download figure:
Standard image High-resolution imageThe cathode was decreased in size to D = 1 cm (open symbols), and two main differences in the potential distribution were observed (Fig. 5c). First, the ohmic drop became nearly negligible, with a maximum of 5 mV difference between Eedge and Ebase along all r values tested. Second, all potentials within the system were more negative in value, indicating that the smaller cathode size was not able to polarize the pit to the degree of the larger cathode size. This lack of polarization lowered the critical radius for stable growth (rcrit ) from 420 μm to 61 μm as indicated in Fig. 5d.
The current density distribution along the same hemispherical pit surface with r = 15 μm can be seen in Fig. 6a. The total anodic current was determined by integrating the current density over the active anodic surface area. Results were then overlaid on the maximum pit model for 3 M NaCl as a function of r, to compare the FEM results with the predicted stability of the third criterion,  These results are the curves labeled with the different diameters. The calculated current from the FEM model (IFEM) predicted active pit growth for r < 25 μm, when under 50% saturation for a constant WL = 16 μm and D = 15 cm (Fig. 6b). The impact of deviations of D both above and below the 15 cm baseline were calculated, and these led to proportional changes to both IFEM and rcrit
, indicating that a larger cathode size produces the highest current and the most stable pits via the largest rcrit
(Fig. 6b).
These results are the curves labeled with the different diameters. The calculated current from the FEM model (IFEM) predicted active pit growth for r < 25 μm, when under 50% saturation for a constant WL = 16 μm and D = 15 cm (Fig. 6b). The impact of deviations of D both above and below the 15 cm baseline were calculated, and these led to proportional changes to both IFEM and rcrit
, indicating that a larger cathode size produces the highest current and the most stable pits via the largest rcrit
(Fig. 6b).
Figure 6. 3 M NaCl hemispherical pit, WL = 16 μm, D = 15 cm; (a) 270° current density surface at r = 15 μm; (b) IFEM as a function of r with the maximum pit model.
Download figure:
Standard image High-resolution imageNote the difference between IFEM and  The higher values of
The higher values of  are due the ideal cathode assumption, whereas the FEM assumes a more-realistic cathode which accounts for the spatial distribution of the current. Consequences of this assumption will be discussed in detail in a later section.
are due the ideal cathode assumption, whereas the FEM assumes a more-realistic cathode which accounts for the spatial distribution of the current. Consequences of this assumption will be discussed in detail in a later section.
Raising the WL to 150 μm, while holding the remaining parameters above constant, resulted in an increased rcrit
based on FEM from 25 to 91 μm (Fig. 7a). This analysis was extended to a variety of WL ranging from 10–500 μm. At a constant D = 15  IFEM from a 3 M NaCl hemispherical pit was plotted as the 3-D surface corresponding to combinations of r and WL (Fig. 7b).
IFEM from a 3 M NaCl hemispherical pit was plotted as the 3-D surface corresponding to combinations of r and WL (Fig. 7b).
Figure 7. 3 M NaCl hemispherical pit, D = 15 cm; (a) IFEM at WL = 150 μm as a function of r with the maximum pit model; (b) IFEM as a function of WL and r. Note the circle in (a) and (b) represents the same critical triple points in both plots.
Download figure:
Standard image High-resolution imageThe peak current appears in the top corner of the plot, indicating that the current is proportional to both WL and r. The critical values at 50% salt film saturation which predict the transition from stability to repassivation are plotted as a white line over the contour plot. Each point along this line represents a combination of rcrit , WLcrit, and Icrit at which stability of a pit will occur within a 3 M NaCl environment. At a WL of 150 μm, Icrit and rcrit were seen to be 68 μA and 91 μm, respectively (Fig. 7a). This triple point along the white line is denoted as a circle in Fig. 7b.
To more thoroughly study the effects of D, the parameters r and WL were held constant at 15 μm and 16 μm, respectively, while the diameter range probed was from 1 to 50 cm, affecting the cathode-to-anode surface area ratio by four orders of magnitude. The potential distributions (Eedge, Emouth, and Ebase) diverged at large D values, as shown in Fig. 8a, indicating that the ohmic drop was impacted to a greater extent by variations in the cathode geometry in contrast to the pit geometry. The increase in all potentials at larger D implies that pits will be less stable (more likely to repassivate) at small D values, although in the range of parameters tested, Erp did not predict the repassivation of any pits (Fig. 8a).
Figure 8. 3 M NaCl hemispherical pit, r = 15 μm and WL = 16 μm; (a) potential distribution as a function of D; (b) IFEM as a function of r with the maximum pit model; (c) IFEM as a function of D.
Download figure:
Standard image High-resolution imageThe maximum pit model and IFEM, derived for the same environmental conditions, were plotted for a constant r and WL (Fig. 8b). At D < 9 cm, all pits were predicted to repassivate. As D increased, IFEM also increased, passing through ILC 50% saturation at D = 9 cm, but falling just short of ILC 100% saturation. Although it may seem that D > 50 cm would continue this rising current trend, instead IFEM is seen to be asymptotically approaching ILC 100% saturation (Fig. 8c). At large D values, Eedge quickly approaches  signifying that the cathode is exhausting nearly all of its available current (Fig. 8a). Therefore, in this scenario, if 100% saturation was needed for stability, even an extremely large cathode with finite kinetics used in this work would not be able to consume enough current to achieve stability.
signifying that the cathode is exhausting nearly all of its available current (Fig. 8a). Therefore, in this scenario, if 100% saturation was needed for stability, even an extremely large cathode with finite kinetics used in this work would not be able to consume enough current to achieve stability.
The impact of varying WL and D with a constant r of 15 μm was also investigated. A contour plot was used to visualize the 3-D data, with the IFEM color bar describing the pseudo z-axis contours. As before, the white line represented the set of critical triple points at which stability at 50% saturation was achieved (Fig. 9a).
Figure 9. IFEM as a function of WL and D for a hemispherical pit, r = 15 μm in (a) 3 M NaCl and (b) 0.6 M NaCl.
Download figure:
Standard image High-resolution imageThe pit solution was changed to 0.6 M NaCl, and identical simulations regarding the WL and r parameter space were conducted. There were two important distinctions between the trends seen in 3 M NaCl and 0.6 M NaCl. First, the stable region, as indicated to the right of the critical white line, is smaller in the less concentrated solution. Second, at all parameters tested, IFEM was also lower in this solution for all D and WL (Fig. 9b).
Simple rectangular pit stability
In a 3 M NaCl solution, the stability of a rectangular pit (Fig. 1b) was investigated as a function of both WL and x. For consistency, r and D were held constant at 15 μm and 15 cm, respectively. To have true 1-D diffusion, it is known that x must be about ten times larger than r. 45 In the given scenario, this constraint bounds x to values larger than 150 μm; however, a benefit of the FEM model is the ability to go beyond what may be physical constraints. Therefore, the range of pit depths tested was from 1 to over 43 times the radius of the pit.
Galvele's (i·x) was utilized as the stability criterion to account for the new pit dimensionality. Therefore, contours of the calculated current density multiplied with the varied pit depth, rather than the total current, were plotted as a function of WL and x (Fig. 10). In this way, (i·x)crit follows a singular contour line of 0.25 A/m. To better visualize the white stability line representing the triple points of WLcrit, xcrit, and (i·x)crit, a magnified portion of the contour plot was inlaid. The majority of the selected parameter space predicted a stable growing pit. Repassivation was only achieved at extremely low WL and x; far below what is accepted as 1-D behavior (Fig. 10).
Figure 10. (i·x)crit stability as a function of WL and x for a rectangular pit, r = 15 μm and D = 15 cm  in 3 M NaCl.
in 3 M NaCl.
Download figure:
Standard image High-resolution imageGeometrically complex pit stability
The geometries within the model were modified to represent irregular, but realistic, pits. In all scenarios going forward, only a 3 M NaCl environment was considered, as it was determined in the previous section to produce the most stable pits. As each parameter was varied, the other parameters were always held constant at r = 15 μm, WL = 16 μm, and D = 15 cm, unless otherwise noted.
A pit-within-a-pit was built, as one step towards increasing the complexity relative to the simple hemispherical geometry (Fig. 1c). This simulation represents a new pit growing in a region where a previously active pit has repassivated, creating a deeper overall pit depth. Only the secondary pit had active anodic surfaces, with rsecondary = 0.5(rprimary ); both pit radii were changed with respect to this relationship. When the "pit radius (r)" is referenced in this geometry, it is referring to the opening of the primary pit, unless otherwise noted.
At a constant r = 15 μm, the potential distribution within the double pit is shown in Fig. 11a. Colored dots represent the points at which the potential was extracted as r was increased from 15 to 150 μm. The potential distributions from the simple hemispherical pit as a function of r were included as dotted lines to easily compare the different geometries. Results indicated that the double pit geometry had negligible effects on Eedge and Ebase in comparison to the hemispherical geometry (Fig. 11b). However, Emouth was much more positive in the double pit than the simple hemispherical geometry. This result is likely due to the primary pit not being active, and therefore the mouth of the primary pit being polarized by the cathode to a higher potential. The maximum pit model and IFEM were plotted with the radius of the complex geometry being with respect to the secondary pit (Fig. 11c). When plotted in terms of the radius of the secondary pit, the pit stability, as determined by  was identical to that of a hemispherical pit of the same radius.
was identical to that of a hemispherical pit of the same radius.
Figure 11. (a) Potential distribution in a double pit, WL = 16 μm, r = 15 μm, and D = 15 cm; (b) comparison of potential distribution between simple hemispherical pit and complex double pit; (c) IFEM as a function of r for hemisphere and double pit geometries, with the maximum pit model. Note the blue, red, and black spheres in (a) represent the points at which the potential was calculated in (b).
Download figure:
Standard image High-resolution imageLastly, the undercutting pit geometry was considered to represent a pit that initiated in a hemispheric geometry but subsequently propagated underneath the surface (Fig. 1d). Particular portions of the pit surface were defined to be anodically active while other regions within the pit were defined as inert. The regions were defined by red bisectors and were labeled numerically in Fig. 12a. Note that the different numerical regions of the pit had different surface areas. Again, the correlative hemispherical pit results were included as hollow points, for comparative purposes (Figs. 12b, 12c, and 12d).
Figure 12. (a) Graphical illustration of different regions in undercut pit, along with points at which the potential was calculated; (b) potential distribution in undercut pit, WL = 16 μm, r = 15 μm, and D = 15 cm; (c) potential distribution in undercut pit, WL = 1,000 μm, r = 15 μm, and D = 15 cm; (d) IFEM from different regions active within the undercut pit compared with maximum pit stability predictions for 50% and 100% saturation. Note the blue, red, teal, and black spheres in (a) represent the points at which the potential was calculated in (b) and (c).
Download figure:
Standard image High-resolution imageThe potential distributions between these different regions were evaluated at a r, and D, with WL = 16 μm in Fig. 12b and WL = 1,000 μm in Fig. 12c. All potentials fell within the bounds of  and Erp, indicating that the first criterion would predict all stable pit propagation for the given parameters. In the thin WL system, there were not any large fluctuations in Eedge between any of the scenarios tested, despite the nearly 50 mV available in the system before reaching
and Erp, indicating that the first criterion would predict all stable pit propagation for the given parameters. In the thin WL system, there were not any large fluctuations in Eedge between any of the scenarios tested, despite the nearly 50 mV available in the system before reaching  which would indicate that the cathode was not at its full capacity to polarize the pit. In comparison, Eedge was very dependent on the location of the active regions when in a bulk WL = 1,000 μm.
which would indicate that the cathode was not at its full capacity to polarize the pit. In comparison, Eedge was very dependent on the location of the active regions when in a bulk WL = 1,000 μm.
At two constant WL of 16 and 1,000 μm, IFEM was compared with  and
and  (Fig. 12d). As seen previously, a larger WL (1,000 μm) increased IFEM, which in turn increased the stability, even to the point of satisfying ILC 100% saturation in this scenario. However, the jump in pit stability was much more dramatic when external regions (such as regions 1 and 2) were active. Conversely, there was a minimal increase in stability when more occluded regions were active, such as regions 4, 5, and 6. When active, region 3 appeared to have the best resemblance to the hemispherical pit, in both the potential distribution and current. As the depth of the active region was very similar to that of the hemisphere, the resulting ohmic drop was nearly identical as well.
(Fig. 12d). As seen previously, a larger WL (1,000 μm) increased IFEM, which in turn increased the stability, even to the point of satisfying ILC 100% saturation in this scenario. However, the jump in pit stability was much more dramatic when external regions (such as regions 1 and 2) were active. Conversely, there was a minimal increase in stability when more occluded regions were active, such as regions 4, 5, and 6. When active, region 3 appeared to have the best resemblance to the hemispherical pit, in both the potential distribution and current. As the depth of the active region was very similar to that of the hemisphere, the resulting ohmic drop was nearly identical as well.
Discussion
Importance of choosing Pit stability criteria
Three stability criteria were investigated in this work: Erp, (i·x), and 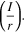 All criteria describe a threshold for reaching and maintaining a critical solution chemistry required for stable pit growth albeit from two perspectives. Considered to be the lowest potential at which a critical chemistry at the pit mouth can be maintained, Erp indicates that any polarization above this point would result in nucleation and growth of pits.
5
Experimental measurements have found that Erp decreases with increasing pit depth, until reaching a plateau at sufficiently deep pits which is considered the "true" Erp.
22
The (i·x) approach instead focuses on the accumulation of complexed salts and acid as corrosion by-products, which form at the base of the pit. Only once a critical fraction of species has been reached, can pits maintain their chemistry against the natural diffusional outflow of the pit. Recent experimental and computational data have found that the critical saturation required (f) is about 50% that of a fully saturated and formed salt film.
22,26
A mathematical maximum pit model takes into account both of these stability criteria to determine the size of an ideal, maximum pit, where
All criteria describe a threshold for reaching and maintaining a critical solution chemistry required for stable pit growth albeit from two perspectives. Considered to be the lowest potential at which a critical chemistry at the pit mouth can be maintained, Erp indicates that any polarization above this point would result in nucleation and growth of pits.
5
Experimental measurements have found that Erp decreases with increasing pit depth, until reaching a plateau at sufficiently deep pits which is considered the "true" Erp.
22
The (i·x) approach instead focuses on the accumulation of complexed salts and acid as corrosion by-products, which form at the base of the pit. Only once a critical fraction of species has been reached, can pits maintain their chemistry against the natural diffusional outflow of the pit. Recent experimental and computational data have found that the critical saturation required (f) is about 50% that of a fully saturated and formed salt film.
22,26
A mathematical maximum pit model takes into account both of these stability criteria to determine the size of an ideal, maximum pit, where  = ILC. The value of
= ILC. The value of 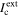 takes into account Erp, while (i·x) is used to calculate ILC.
takes into account Erp, while (i·x) is used to calculate ILC.
In this work, Erp and (i·x) are compared separately to data calculated through the FEM model. A comparison of Emouth with Erp was conducted to assess the first stability criterion. To isolate Galvele's (i·x) criterion in the maximum pit model, the simulated data were compared to ILC only. Therefore, ILC 50% saturation correlates directly to  the third stability criterion. It was determined that the stability from both criteria scaled directly with WL and D, and inversely with r and x (Figs. 5–10). For example, large r values are more likely to repassivate due to the potential distributions approaching Erp as r increases (Fig. 5c). A similar result is seen when comparing the current with the second stability criterion, such as in Fig. 7b. Any combination of parameters to the left of the white line (such as small r values) would predict a stably propagating pit, whereas any combination of parameters to the right of the white line (such as large r values) would predict pit repassivation, for a given D (Fig. 7b). However, when WL and D were concurrently changed (Fig. 9b), parametric combinations to the left of the critical white line (such as small D and small WL) predicted repassivation while combinations to the right of the white line (such as large D and large WL) predicted stable growth. Experimental results from literature confirm that larger WL (200–400 μm) are more favorable for stable pit growth, whereas smaller WL (5–10 μm) require a higher chloride concentration before stability can occur.
46
The same methodology as above can be applied to Fig. 10 to see the correlation with pit stability and x.
the third stability criterion. It was determined that the stability from both criteria scaled directly with WL and D, and inversely with r and x (Figs. 5–10). For example, large r values are more likely to repassivate due to the potential distributions approaching Erp as r increases (Fig. 5c). A similar result is seen when comparing the current with the second stability criterion, such as in Fig. 7b. Any combination of parameters to the left of the white line (such as small r values) would predict a stably propagating pit, whereas any combination of parameters to the right of the white line (such as large r values) would predict pit repassivation, for a given D (Fig. 7b). However, when WL and D were concurrently changed (Fig. 9b), parametric combinations to the left of the critical white line (such as small D and small WL) predicted repassivation while combinations to the right of the white line (such as large D and large WL) predicted stable growth. Experimental results from literature confirm that larger WL (200–400 μm) are more favorable for stable pit growth, whereas smaller WL (5–10 μm) require a higher chloride concentration before stability can occur.
46
The same methodology as above can be applied to Fig. 10 to see the correlation with pit stability and x.
Note also a distinction in the critical white line between Figs. 7b and 9. Because ILC 50% saturation is dependent on the pit geometry, i.e. Icrit changes at each new r, the white line is not parallel to the current contours in Fig. 7b. However, the critical white line follows the contours in Fig. 9a, rather than going across them. This trend derives from the fact that ILC 50% saturation is independent of both WL and D. That is, the  criterion is constant for these parameters. As each of the contours represents a constant current value, it follows that Icrit would also abide by the contours.
criterion is constant for these parameters. As each of the contours represents a constant current value, it follows that Icrit would also abide by the contours.
Although the two stability criteria had similar correlations with the parameters of interest, that is where the commonalities ended. The Erp criterion predicted much larger rcrit
values when compared to the 3-D pit stability criterion. At a constant D and WL of 15 cm and 16 μm, respectively, Erp predicted rcrit
to be 420 μm (Fig. 5c), whereas  predicted rcrit
to be 25 μm (Fig. 6b). Under the same set of conditions, the maximum pit model approximated
predicted rcrit
to be 25 μm (Fig. 6b). Under the same set of conditions, the maximum pit model approximated  = 78.75 μm through utilization of both stability criteria (Fig. 4a). This result places
= 78.75 μm through utilization of both stability criteria (Fig. 4a). This result places  between the critical radii calculated from each stability criterion alone, although not equidistant. However, the maximum pit model provides the theoretical limit for cathodic current capacity, implying that there can be no pits greater than
between the critical radii calculated from each stability criterion alone, although not equidistant. However, the maximum pit model provides the theoretical limit for cathodic current capacity, implying that there can be no pits greater than  at a given set of conditions. As the geometric parameters were all consistent through the calculations, there are only two parameters to consider which may be incorrect, (1) the critical percent saturation chosen, or (2) the repassivation potential. To reconcile the predicted rcrit
value from the two stability criteria using the critical percent saturation, it was calculated that the solution would only need to be 7% saturated, rather than the 50% saturation used in this work. However, assuming instead that the percent saturation was correct, an Erp = −0.154 VSCE would be required to reconcile the predicted rcrit
.
at a given set of conditions. As the geometric parameters were all consistent through the calculations, there are only two parameters to consider which may be incorrect, (1) the critical percent saturation chosen, or (2) the repassivation potential. To reconcile the predicted rcrit
value from the two stability criteria using the critical percent saturation, it was calculated that the solution would only need to be 7% saturated, rather than the 50% saturation used in this work. However, assuming instead that the percent saturation was correct, an Erp = −0.154 VSCE would be required to reconcile the predicted rcrit
.
The considerably large discrepancy in pit stability as calculated through Erp and  persisted throughout all parameter space tested, although the difference was not consistent. In Fig. 6b, D was lowered from 15 cm to 5 cm, resulting in a 79% decrease in rcrit
as predicted by
persisted throughout all parameter space tested, although the difference was not consistent. In Fig. 6b, D was lowered from 15 cm to 5 cm, resulting in a 79% decrease in rcrit
as predicted by 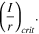 The potential distribution was also calculated with the parameters above and rcrit
as defined by Emouth > Erp was seen to decrease by 41%. These results signify that the
The potential distribution was also calculated with the parameters above and rcrit
as defined by Emouth > Erp was seen to decrease by 41%. These results signify that the  criterion is more sensitive to parametric changes than the Erp criterion. Note that in the pseudo 1-D pit, both Erp and (i·x)crit predicted stable growth in nearly all scenarios, preventing a comparison of the two criteria.
criterion is more sensitive to parametric changes than the Erp criterion. Note that in the pseudo 1-D pit, both Erp and (i·x)crit predicted stable growth in nearly all scenarios, preventing a comparison of the two criteria.
Consequences of an ideal cathode assumption
A common method of studying pitting in materials is through the use of potentiostatic holds, in which increased currents directly correlate to metastable (if transient spikes) or stable pit initiation/growth whereas a sharp decrease to the current indicates repassivation. 4,6,47,48 Although useful in extracting pit kinetics over a wide range of potentials, potentiostatic conditions imply an infinite cathode in which pits are only limited anodically; this condition is often not seen in service. To attain the most realistic measurements, the material of interest should be at open circuit conditions where the conservation of charge applies, usually expressed as ∑Ia = ∑ Ic. Under these conditions, the total anodic current (Ia) comes from the pit(s) with a small contribution from the surrounding passive surface while the cathodic current (Ic) is a combination of the external cathodic reaction occurring on the surfaces surrounding the pit and local cathodic reactions within the pit itself. 30 As both the anode and the cathode are finite, either can act as the limiting factor in stifling pit growth.
The maximum pit model takes one step towards modeling a more realistic cathode by including both anodic and cathodic limitations in pit development.
27
One of the main assumptions of the maximum pit model is that all positions along the cathode provide a constant current density, determined by integrating the cathodic polarization from  to Erp. As stated previously, this idealized, equivalent cathode assumption provides a theoretical limit of cathodic current and allows for the calculation of rmax for a given set of environmental conditions. To gain information on pits that are not at their theoretical limit, a spatial distribution of current density is needed, with the peak current density expected to be nearest to the pit mouth.
to Erp. As stated previously, this idealized, equivalent cathode assumption provides a theoretical limit of cathodic current and allows for the calculation of rmax for a given set of environmental conditions. To gain information on pits that are not at their theoretical limit, a spatial distribution of current density is needed, with the peak current density expected to be nearest to the pit mouth.
Rather than assuming either an infinite or an ideal cathode, this work aims to describe a realistic cathode in a pitting scenario in which the current density is not constant with position. The potential along the cathode was also not assumed to be constant, but rather the gradient between the less-negative cathode edge and more-negative pit mouth was calculated (Fig. 5b). Experimentally determined PDS were used as boundary conditions for both the cathode and the anode, to capture the active kinetics which take place during the pitting process. To estimate the level of conservatism that comes with an ideal cathode assumption, rcrit (as calculated through the FEM model in this work) and rmax (as calculated from the maximum pit model) were compared.
At a variety of different D values, rcrit
was calculated via FEM in 3 M NaCl for a constant WL of 16 μm (Fig. 13). That is, rcrit
was determined through the same procedure as described for Fig. 6b. The predicted  under the same conditions as above was included in the plot as a horizontal line, though the maximum ideal cathode (Dmax) for these conditions is predicted to be 12.8 cm. Although the FEM model simulated D values out to 65 cm, nearly 5 times of that needed by an ideal cathode, rcrit
never reached the predicted rmax but instead plateaued at D ≈ 45 cm (Fig. 13). This result suggests that the theoretical estimate of rmax is conservative by about a factor of 2 under these conditions. Interestingly, a similar comparison between the maximum pit model and outdoor exposure testing on SS316 is seen in literature.
27
Although the experimental exposures of pit depth varied with location and exposure time, a comparison of the averaged exposure values with rmax
calculation also demonstrates the maximum pit model overestimating the experimental results by a factor of two.
27
under the same conditions as above was included in the plot as a horizontal line, though the maximum ideal cathode (Dmax) for these conditions is predicted to be 12.8 cm. Although the FEM model simulated D values out to 65 cm, nearly 5 times of that needed by an ideal cathode, rcrit
never reached the predicted rmax but instead plateaued at D ≈ 45 cm (Fig. 13). This result suggests that the theoretical estimate of rmax is conservative by about a factor of 2 under these conditions. Interestingly, a similar comparison between the maximum pit model and outdoor exposure testing on SS316 is seen in literature.
27
Although the experimental exposures of pit depth varied with location and exposure time, a comparison of the averaged exposure values with rmax
calculation also demonstrates the maximum pit model overestimating the experimental results by a factor of two.
27
Figure 13. Critical hemispherical pit radius as a function of critical cathode radius, with WL = 16 μm, as calculated via the FEM model using  as the pit stability criterion, in 3 M NaCl; the horizontal red dashed line represents rmax at 50% saturation in the same conditions, while the vertical red dashed line represents Dmax, as predicted by the maximum pit model.
as the pit stability criterion, in 3 M NaCl; the horizontal red dashed line represents rmax at 50% saturation in the same conditions, while the vertical red dashed line represents Dmax, as predicted by the maximum pit model.
Download figure:
Standard image High-resolution imageAnother interesting point is the extreme size required for a realistic cathode to achieve its full current capacity. The maximum pit model predicts that if a cathode was perfectly consuming all of the available current from one single r = 15 μm pit, the cathode diameter D would only need to be 12.8 cm for a WL = 16 μm. However, a 12.8 cm realistic cathode does not behave ideally, as evident by the lack of polarization of Eedge at D = 12.8 cm (Fig. 8a). Not until D values of nearly 45 cm is the entire current capacity being used, and even at these large dimensions the total current is nearly 50% less than the predicted current from a 12.8 cm idealized cathode as stated above (Fig. 8b). That is to say, the FEM model predicts D = 45 cm is needed to provide the full current capacity to one pit. This prediction assumes that no other pits are present within this diameter, as then the cathode current would be shared among all active pits. Experimentally, however, Budiansky et al. have shown that pits interact and form clusters on a SS316 surface at much smaller size scales. 49 Furthermore, experimental samples used to study pitting behaviors usually range from 10's of μm-sized wires to planar samples on the mm-scale. 4,6,11,12,49,50 The results from this work indicate that those sample sizes will not be able to provide the maximum amount of available current under open circuit conditions, which may underpredict the worst-case pitting scenario. An additional challenge to achieving these values of D in service is the low probability that a WL of 16 μm would be maintained over such a large distance.
Environmental influences on pit stability
Pit stability in different environments has been widely studied, varying from different aggressive solutions 6,7,13,21–23,27,28,33 and temperature impacts, 13,23,51 to a variety of WL. 28,46,50 This work conducts an initial analysis of environmental impact by extending the current framework to a lower chloride concentration and a 500 μm range of WL.
A decrease in stability occurred when the chloride concentration was decreased from 3 M NaCl to 0.6 M NaCl, representing an increase in equilibrium RH of 88.3% to 98%, respectively (Fig. 9). Multiple factors contributed to this reduction of stability. When maintaining a constant WL and transitioning from a solution of 3 M NaCl to 0.6 M NaCl, an increase in  occurs, from 0.75 A m−1 to 1.35 A m−1, respectively, as inferred from Table I. Correspondingly, rmax is lowered under these conditions, as both
occurs, from 0.75 A m−1 to 1.35 A m−1, respectively, as inferred from Table I. Correspondingly, rmax is lowered under these conditions, as both  and ILC are dependent on the chloride concentration (Fig. 4). This direct correlation between rmax and chloride concentration at a constant temperature is consistent with what has been seen in literature.
23
and ILC are dependent on the chloride concentration (Fig. 4). This direct correlation between rmax and chloride concentration at a constant temperature is consistent with what has been seen in literature.
23
A decrease in IFEM was seen in 0.6 M NaCl, making it more difficult to achieve the higher  threshold, thereby lowering the stability (Fig. 9). Although a difference in kinetics is usually the main culprit when impacting the current within a constant geometry, in this scenario that was not the case. The PDS revealed very similar kinetics behavior between the two environments, with only a 7 μA cm−2 difference between the galvanic coupling currents for a 1:1 cathode-to-anode area ratio (Fig. 3). However, κbulk between the 3 M NaCl and 0.6 M NaCl solutions differed by 14 S m−1, (a factor of 3.6), indicating that the decreased IFEM was due to increased ohmic drop rather than slow kinetics. This result highlights the impact that κbulk can have on the stability of a pit, and is consistent with Katona et al.'s finding that lower conductivity solutions (MgCl2 in contrast to NaCl) decrease the severity of pitting.
52
threshold, thereby lowering the stability (Fig. 9). Although a difference in kinetics is usually the main culprit when impacting the current within a constant geometry, in this scenario that was not the case. The PDS revealed very similar kinetics behavior between the two environments, with only a 7 μA cm−2 difference between the galvanic coupling currents for a 1:1 cathode-to-anode area ratio (Fig. 3). However, κbulk between the 3 M NaCl and 0.6 M NaCl solutions differed by 14 S m−1, (a factor of 3.6), indicating that the decreased IFEM was due to increased ohmic drop rather than slow kinetics. This result highlights the impact that κbulk can have on the stability of a pit, and is consistent with Katona et al.'s finding that lower conductivity solutions (MgCl2 in contrast to NaCl) decrease the severity of pitting.
52
Variations in WL were also investigated in a 3 M NaCl solution, as a function of both, x and D. For a given geometry, IFEM becomes independent of WL beyond a certain threshold value as shown by near-vertical contour lines in Figs. 7b, 9a, and 10. For example, at an arbitrary x = 100 μm, WL > 50 μm have a negligible effect on IFEM (Fig. 10). As x (or r) increases, the threshold for WL impact increases as well. Although an interesting observation, this parameter independence did not impact the pit stability.
However, when the critical white line was directly correlated to the contour lines (such as in Fig. 9a), the pit stability was impacted by the near-vertical contour line, which indicated WL independence. That is, only extremely small WL (on the order of a few microns in a 3 M NaCl solution) at D > 6.5 cm could prevent the stability of a pit; all other WL will have no contribution in determining pit growth or repassivation. In a 0.6 M NaCl solution, much larger WL ≈ 100 μm could have an impact on stability, implying that in lower chloride concentrations (and correspondingly higher RH) WL may play a more significant role in pit stability as opposed to 3 M NaCl solutions (Fig. 9b).
Dimensionality impact of the anode and cathode on Pit stability
The impact of r on stability has been well documented in literature. 11,20,21,48 Using the FEM model, this work has confirmed that smaller pits are more stable via their lower current demand, and are less likely to grow into larger pits where the higher current demand cannot be maintained (Figures 5–7). Additionally, the decrease in potential as a function of r demonstrates a much larger polarization than predicted from an ideal pit (Fig. 5c). Although thorough studies on r are common, less work has been conducted on the impact of the cathode geometry.
An important parameter in maintaining stability, D was able to both polarize the system above Erp (Fig. 5c), and consume current (Fig. 6b). Indeed, when WL and D were changed concurrently in 3 M NaCl, the importance of D was magnified (Fig. 9a). At D = 6.5 cm, this parameter became nearly the sole criteria for stability, indicating that any small deviations could determine the final outcome of a metastable pit. An interesting point to note is that in 0.6 M NaCl, a stability region existed around WL = 100 μm which was independent of D (Fig. 9b). That is, at this WL, variations in D would have little effect on the pit stability.
Implications of the pit geometry
Although this work focused on a simple hemispherical pit, the nature of the model allowed for the pit geometry to be transformed while keeping all other boundary conditions and assumptions constant. A pseudo-1-D pit, represented in 2-D as a rectangle and in 3-D as a cylinder, was the first geometry to be compared (Fig. 1b). This geometry displayed impressive stability in terms of both Erp and (i·x)crit (Fig. 10). While the potential distributions in this geometry are not shown, Emouth > Erp for the range of pit depths tested, up to x = 1,000 μm.
At first glance, the rectangular pit seems much more likely to stably grow as opposed to a hemispherical pit, however, caution must be taken. Geometrically, r (of the hemisphere) and x (of the 1-D pit) represent the same pit depth, as r ≡ x along the z-axis. The pit depths were tested with the same range of r = x = (15 μm to 500 μm). The caveat being the that the total anodic surface areas were not equal; the hemispherical anodic surface scaled with r2 while the active surface area in the 1-D pit remained constant.
The total anodic surface area can impact the anodic demand for current, making a comparison between pit stability rather difficult. One similarity that can be made, however, involves WL. In both geometries, WL has little effect on IFEM, or (i·x) in the case of the 1-D pit, as represented by the vertical contours (Figs. 9 and 10).
The remaining two pit geometries considered were complex deviations of a basic hemispherical design (Figs. 1c and 1d). These pits were chosen to represent porosity and roughness features typically observed in/on AM surfaces. 53,54 The roughness of stainless steel surfaces has been shown to play an important role in pitting. Literature has demonstrated an inverse correlation between the critical pitting temperature and the surface roughness, indicating that pitting occurs more easily on a rougher surface, possibly via an increase in the effective diffusion path making it easier to maintain the aggressive chemistry in an occluded site. 51,55 In a 3 M NaCl environment, as-printed powder bed fusion (PBF) and selective laser melting (SLM) SS316 samples were seen to have a higher affinity for pitting, as opposed to wrought SS316, further highlighting the importance of surface roughness. 6,53 Moreover, the shape of the individual pits has been postulated to have a large impact on stability, via differences in the degree of occlusion controlling the retention of the aggressive species. Duan et al. found experimentally that a covered gas pore, akin to the undercut pit geometry, transitions to stable growth more easily than an open gas pore, i.e., a simple hemispherical pit. 6
Therefore, in this work, a double pit and undercut pit geometry were investigated (Figs. 1c and 1d). The double pit geometry expanded on a simple hemispherical design by representing an active pit growing inside of a previously repassivated pit. Experimentally, it has been shown that repassivated pits are still a valid location for active pits to nucleate and grow.
7,56,57
In the context of AM, this scenario also corresponds to a gas pore with an affinity for pitting initiation.
6
The active surface, labeled the "secondary pit," was half of the radius of the repassivated surface, labeled the "primary pit." The opening of the secondary pit  was 60% of the radius, rsecondary
, in all studies (Fig. 1c).
was 60% of the radius, rsecondary
, in all studies (Fig. 1c).
The last complex geometry considered was made to represent the phenomenon of undercutting pits which have been seen to occur in stainless steels.
7,53,58
An obtrusion was included at the pit mouth to account for an additional surface defect, such as a partially melted powder particle from the AM process (Fig. 1d).
53
Within the undercut pit, additional simulations were conducted by varying the active regions (Fig. 12). Defining particular locations in the pit to be anodically active while other features within the pit are inert could be useful in future work to determine which facets, on a real as-printed surface, may be the most likely to maintain pit stability. To easily compare the effects of these features, the current calculated in all hemispherical-based pit simulations were plotted together, as a function of WL. Both saturation conditions,  and
and  were included as red and black dashed lines, respectively (Fig. 14).
were included as red and black dashed lines, respectively (Fig. 14).
Figure 14. IFEM for all hemispherical-based pits as a function of WL, with r = 15 μm, and D = 15 cm; black and red horizontal dashed lines represent the pit stability criterion at 50% and 100%, respectively. Arrows denote dominant regions of ohmic drop either within the pit (interior) or outside of the pit (exterior).
Download figure:
Standard image High-resolution imageThe second criterion  through using ILC 50% saturation, was satisfied WL ≈ 10 μm for all geometries except for the double pit. However, as WL increased, IFEM of each unique pit scenario diverged, spanning a range of 32 μA. The repercussions of the divergence are clearly seen if ILC 100% saturation was needed to obtain stability. For example, the undercut pit with all regions active could obtain stable growth at WL = 20 μm, as seen by the intersection of IFEM and ILC 100% saturation. However, for a hemispherical pit in that same scenario, WL = 42 μm is required. If an undercut pit had only the side walls active, as represented by region 5, then an even larger WL = 70 μm is required to maintain stable growth at ILC 100%.
through using ILC 50% saturation, was satisfied WL ≈ 10 μm for all geometries except for the double pit. However, as WL increased, IFEM of each unique pit scenario diverged, spanning a range of 32 μA. The repercussions of the divergence are clearly seen if ILC 100% saturation was needed to obtain stability. For example, the undercut pit with all regions active could obtain stable growth at WL = 20 μm, as seen by the intersection of IFEM and ILC 100% saturation. However, for a hemispherical pit in that same scenario, WL = 42 μm is required. If an undercut pit had only the side walls active, as represented by region 5, then an even larger WL = 70 μm is required to maintain stable growth at ILC 100%.
The double pit exhibited a much lower IFEM than the remaining geometries. Recall that the active secondary pit had a radius half the size of all other pit radii, so it follows that the active anodic surface area would be the smallest in comparison to the remaining geometries. Rerunning the simulation as a function of WL with rsecondary = 15 μm and rprimary = 30 μm, that is, with rsecondary equal to the opening of the other pit geometries, IFEM was increased within the range of the other geometries seen in Fig. 14. However, for the consistency of all initial pit openings being equal, the lower surface area result remained included.
One main conclusion deduced from Fig. 14 is that at thin WL (5 to 20 μm), the ohmic drop outside of the pit is the limiting factor dominating IFEM. This conclusion is evident by the negligible effects of the pit geometries at these thin WL. However, as the WL increases, ohmic drop inside of the pit becomes more important. At larger WL (> 100 μm), IFEM is nearly constant but distinct between each individual pit geometry, indicating that the ohmic drop inside the pit is dominant and limiting the current. Distinctions within the constant IFEM values are attributed to a difference in anodic surface area in each simulation, as discussed with the double pit geometry above.
Looking specifically at the undercut pit simulations, the contributions of the ohmic drop could be seen from a different perspective. The potential distribution in a thin WL = 16 μm revealed the largest amount of ohmic drop was always outside of the pit (difference between Eedge and Emouth,b), regardless of which region was active (Fig. 12b). However, at bulk WL (1,000 μm), the largest ohmic drop was always inside of the pit (difference between Ebase and Emouth,a), except when regions 1 or 2 were active (Fig. 12c).
By testing a variety of scenarios, the impact of the ohmic drop on the individual regions could further be evaluated. Regions 1 and 2 were active exterior surfaces, and therefore did not have any ohmic drop within the pit. More secluded regions (such as regions 4, 5 and 6) always had a larger interior ohmic drop in all WL than region 3 or the hemispherical pit, due to the longer diffusion path. The diffusion path was comparable between region 3 and the hemispherical pit, and therefore both scenarios had similar potential distributions and total currents.
Larger WL corresponded to an increase in IFEM for all scenarios (Fig. 12d). However, at small WL = 16 μm IFEM across all scenarios was very similar, with 6.8 μA of variance, in comparison to WL = 1,000 μm which enlarged the disparity in IFEM to 27 μA, an increase by a factor of four. The disparity in IFEM across the different scenarios was increased in the larger WL because the active regions dominated by an exterior ohmic drop (regions 1 and 2) accrued much more current than those dominated by an interior ohmic drop (regions 4, 5, and 6). Therefore, it can be inferred that the ohmic drop outside of the pit is more dependent on WL, then the ohmic drop inside of the pit. In practical terms, the pit geometry has a greater impact on stability when thicker WL are present (>100 μm in our scenario), as opposed to thinner WL in which all geometries behave hemispherically.
Limitations
Although the current framework is useful, it includes simplifying assumptions which should be appreciated. The governing equation assumes a steady-state system and does not take into account any chemical reactions, pH, or κ variations. Additionally, the WL is assumed to be uniform, which neglects the possibility of imperfect wetting or a discontinuous droplet layer. A recent review by Herman Terryn and coworkers highlights the impact that WL geometry can have on modeling results. 59
The PDS boundary conditions within the model also include an important caveat, that they were conducted on wrought SS316 surfaces. Although the application of this complex pit stability work can be generalized to AM or irregular wrought SS316 surfaces, the boundary conditions which were used did not technically portray the kinetics of an AM SS316 surface. The level to which these boundary conditions impact the results is currently being investigated. Further work will involve the generation of electrochemical boundary conditions on AM SS316 surfaces to capture the correct kinetics for this application.
Limitations of the pit stability criteria should also be considered. When predicting the stability of a simple 1-D or 3-D hemispherical pit, determining which threshold criteria to use is straightforward, with a geometric factor of 3 acting as the conversion of the pit stability product.
4,16,17,19
However, as more details within a 3-D pit geometry are included, using  as a threshold for stability may no longer be an accurate assumption due to both a change in surface area and a possible non-uniform rate of propagation. No derivation exists, that the authors are aware of, which converts (i·x) or
as a threshold for stability may no longer be an accurate assumption due to both a change in surface area and a possible non-uniform rate of propagation. No derivation exists, that the authors are aware of, which converts (i·x) or  to complex non-hemispherical pit geometries. However, in one instance to account for an undercut pit, Ghahari et al. used a modified (i·x) stability criterion which multiplied the current by the local pit depth, rather than the overall pit radius.
7
In this work, the conventional
to complex non-hemispherical pit geometries. However, in one instance to account for an undercut pit, Ghahari et al. used a modified (i·x) stability criterion which multiplied the current by the local pit depth, rather than the overall pit radius.
7
In this work, the conventional  is assumed to be applicable as a stability criterion for all hemispherical-based pit geometries. On the other hand, Erp is applicable to all pit geometries; measurements of Eedge in bulk samples and artificial 1-D pits revealed similar values.
5
Relying on Erp to predict stability, however, may result in much larger rcrit
estimations than predicted by
is assumed to be applicable as a stability criterion for all hemispherical-based pit geometries. On the other hand, Erp is applicable to all pit geometries; measurements of Eedge in bulk samples and artificial 1-D pits revealed similar values.
5
Relying on Erp to predict stability, however, may result in much larger rcrit
estimations than predicted by  as discussed in a previous section of this work. If both criteria are accurate, then Erp is providing a more conservative, and
as discussed in a previous section of this work. If both criteria are accurate, then Erp is providing a more conservative, and  a more stringent, prediction of stability. Current work is underway to determine a less conservative value of the Erp.
a more stringent, prediction of stability. Current work is underway to determine a less conservative value of the Erp.
Note that an additional pit stability criterion 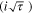 exists, which takes into account the critical time to pit initiation
exists, which takes into account the critical time to pit initiation  48,60,61
Limitations of the steady-state model prevented the use of
48,60,61
Limitations of the steady-state model prevented the use of  in this work, although Li et al. describes how (i·x),
in this work, although Li et al. describes how (i·x),  (described as (ir) in their work), and
(described as (ir) in their work), and  are really all equivalent.
62
are really all equivalent.
62
Lastly, it is of utmost importance to remember that WL variations in this study were all conducted at a constant chloride concentration, in either 3 M NaCl or 0.6 M NaCl. The LD was therefore changed with each new WL under investigation, while RH remained constant. This methodology is in contrast to wet-dry cyclic studies, in which a given WL is evaporated, increasing the chloride concentration, but with a (relatively) constant LD. Experimental wet-dry exposures on stainless steels have found that thinner WL are most aggressive for pitting nucleation and growth, due to restricted diffusion of aggressive species away from the anodic region and a lack of convection. 50 This result may seem to be in direct contrast to the conclusions presented in this work, which state that small WL should result in less stable pits, when in fact they are complimentary. The thinner WL described by Vera Cruz et al. are at a higher chloride concentration than their initial bulk sample. 50 Results from this work have also shown that higher chloride concentrations (3 M NaCl) achieve more stability than their lower counterparts (0.6 M NaCl). Combining these conclusions leads to the theory that chloride concentration is more important to pit stability than WL, although further investigations need to be conducted.
Conclusions
In this work, a finite element method model framework was developed to describe the conditions under which a pit would cross the threshold from metastable to stable pit growth. Different geometries were investigated, to determine the impact of pit shape on pit stability. Each new pit geometry was compared with a baseline hemispherical pit. The environmental impact on pit stability was also investigated through two different chloride concentrations and a range of water layer thicknesses. To determine pit stability, results from the model were compared with the repassivation potential and both the 1-D and 3-D pit stability products. The main conclusions of this work are below:
- A framework was created using experimentally determined potentiodynamic boundary conditions to describe the transition of an actively corroding pit to either stable growth or repassivation, via the comparison of different stability criteria (Erp, (i·x) or
 ). The Erp was found to be more conservative in predicting pit stability, when compared to the pit stability product for a 3-D geometry.
). The Erp was found to be more conservative in predicting pit stability, when compared to the pit stability product for a 3-D geometry. - Between two common simplified pit geometries, it was seen that the pseudo-1-D pit was much more likely to transition to stable growth in all environments than the 3-D hemispherical pit, neglecting any differences in anodic surface area. This may suggest the aspect ratio of processing defects found in AM metals will be the most critical factor when it comes to corrosion susceptibility.
- A thorough study of parameter space determined that the following parameters all lower the stability of a pit, increasing the possibility of repassivation, independent of pit shape: lower chloride concentration, smaller cathode diameter, and smaller water layer thickness. Furthermore, it was confirmed that small hemispherical pits and small 1-D pits are likely to repassivate after a certain pit radius, due to the inability to maintain the higher current demand of the increased pit size.
- Initial results conclude that the maximum current from a realistic cathode is achieved around a diameter of 45 cm, where the open circuit potential is nearly reached, as opposed to an idealized cathode in the same scenario which is predicted to be 12.8 cm. However, this current is still 50% less than the predicted current from an ideal cathode, implying an overestimation of the maximum pit model by a factor of 2 with the parameters tested. This finding was confirmed through a comparison of outdoor exposure with the maximum pit model by Chen & Kelly in 2009. 27
- According to the present model, under atmospheric conditions, the pit geometry does not have a significant impact on the pit stability. That is, the complex-shaped pits generated in this study behave similarly to a simple hemispherical pit in thin water layers (≤ 20 μm) due to the ohmic drop outside of the pit being the limiting factor.
Acknowledgments
This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. This work was supported through a DOE funded ACT program. This document is SAND2022-0335 J. In addition, financial support provided by the NASA Virginia Space Grant Consortium through a Graduate Research Fellowship is gratefully acknowledged.



















